PROPERTIES OF PURE SUBSTANCES:PROPERTY TABLES

PROPERTY TABLES

For most substances, the relationships among thermodynamic properties are too complex to be expressed by simple equations. Therefore, properties are frequently presented in the form of tables. Some thermodynamic properties u can be measured easily, but others cannot and are calculated by using the 1

relations between them and measurable properties. The results of these measurements and calculations are presented in tables in a convenient format. In the following discussion, the steam tables will be used to demonstrate the use of thermodynamic property tables. Property tables of other substances are used in the same manner.

For each substance, the thermodynamic properties are listed in more than one table. In fact, a separate table is prepared for each region of interest such as the superheated vapor, compressed liquid, and saturated (mixture) regions. Property tables are given in the appendix in both SI and English units. The tables in English units carry the same number as the corresponding tables in SI, followed by an identifier E. Tables A–6 and A–6E, for example, list properties of superheated water vapor, the former in SI and the latter in English units. Before we get into the discussion of property tables, we define a new property called enthalpy.

Enthalpy—A Combination Property

A person looking at the tables will notice two new properties: enthalpy h and entropy s. Entropy is a property associated with the second law of thermo- dynamics, and we will not use it until it is properly defined in Chap. 6. How- ever, it is appropriate to introduce enthalpy at this point.

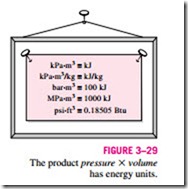
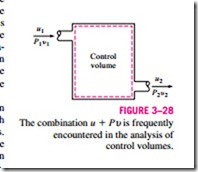
In the analysis of certain types of processes, particularly in power generation and refrigeration (Fig. 3–28), we frequently encounter the combination of properties U + PV. For the sake of simplicity and convenience, this combina- tion is defined as a new property, enthalpy, and given the symbol H:

Both the total enthalpy H and specific enthalpy h are simply referred to as enthalpy since the context will clarify which one is meant. Notice that the equations given above are dimensionally homogeneous. That is, the unit of the pressure–volume product may differ from the unit of the internal en- ergy by only a factor (Fig. 3–29). For example, it can be easily shown that 1 kPa · m3 = 1 kJ. In some tables encountered in practice, the internal energy u is frequently not listed, but it can always be determined from u = h – Pu.

The widespread use of the property enthalpy is due to Professor Richard Mollier, who recognized the importance of the group u + Pu in the analysis of steam turbines and in the representation of the properties of steam in tabular and graphical form (as in the famous Mollier chart). Mollier referred to the group u + Pu as heat content and total heat. These terms were not quite consistent with the modern thermodynamic terminology and were replaced in the 1930s by the term enthalpy (from the Greek word enthalpien, which means to heat).

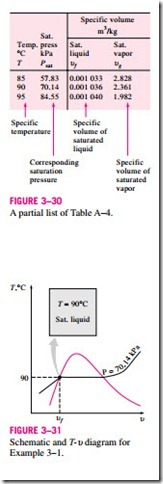
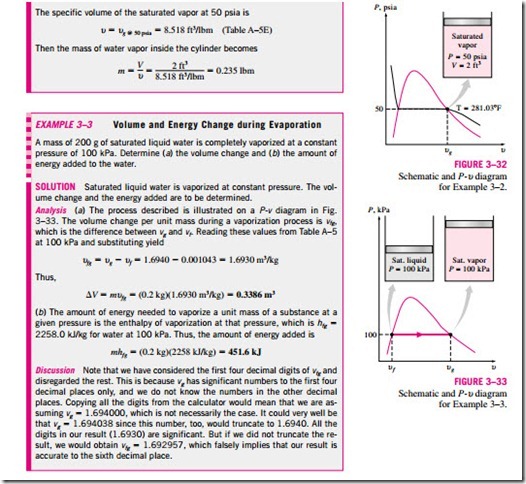
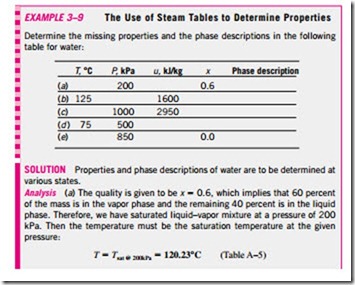
1a Saturated Liquid and Saturated Vapor States The properties of saturated liquid and saturated vapor for water are listed in Tables A–4 and A–5. Both tables give the same information. The only difference is that in Table A–4 properties are listed under temperature and in Table A–5 under pressure. Therefore, it is more convenient to use Table A–4 when temperature is given and Table A–5 when pressure is given. The use of Table A–4 is illustrated in Fig. 3–30.

The subscript f is used to denote properties of a saturated liquid, and the subscript g to denote the properties of saturated vapor. These symbols are commonly used in thermodynamics and originated from German. Another subscript commonly used is fg, which denotes the difference between the saturated vapor and saturated liquid values of the same property. For example,

The quantity hfg is called the enthalpy of vaporization (or latent heat of vaporization). It represents the amount of energy needed to vaporize a unit mass of saturated liquid at a given temperature or pressure. It decreases as the temperature or pressure increases, and becomes zero at the critical point.

1b Saturated Liquid–Vapor Mixture

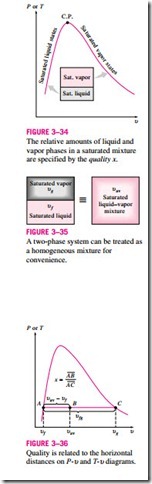
During a vaporization process, a substance exists as part liquid and part vapor.

That is, it is a mixture of saturated liquid and saturated vapor (Fig. 3–34). To analyze this mixture properly, we need to know the proportions of the liquid and vapor phases in the mixture. This is done by defining a new property called the quality x as the ratio of the mass of vapor to the total mass of the mixture:

Quality has significance for saturated mixtures only. It has no meaning in the compressed liquid or superheated vapor regions. Its value is between 0 and 1. The quality of a system that consists of saturated liquid is 0 (or 0 percent), and the quality of a system consisting of saturated vapor is 1 (or 100 percent). In saturated mixtures, quality can serve as one of the two independent intensive properties needed to describe a state. Note that the properties of the saturated liquid are the same whether it exists alone or in a mixture with saturated va- por. During the vaporization process, only the amount of saturated liquid changes, not its properties. The same can be said about a saturated vapor.

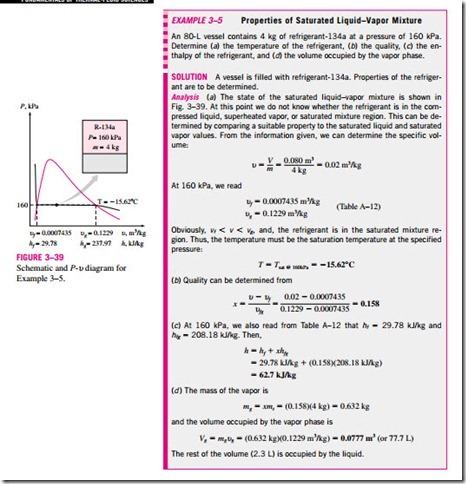
A saturated mixture can be treated as a combination of two subsystems: the saturated liquid and the saturated vapor. However, the amount of mass for each phase is usually not known. Therefore, it is often more convenient to imagine that the two phases are mixed well, forming a homogeneous mixture (Fig. 3–35). Then the properties of this “mixture’’ will simply be the average properties of the saturated liquid–vapor mixture under consideration. Here is how it is done.

Consider a tank that contains a saturated liquid–vapor mixture. The volume occupied by saturated liquid is Vf, and the volume occupied by saturated va- por is Vg. The total volume V is the sum of the two:

a P–u or T–u diagram (Fig. 3–36). At a given temperature or pressure, the nu- liquid state, and the denominator is the length of the entire horizontal line that

quality will lie in the middle of this horizontal line.

The analysis given above can be repeated for internal energy and enthalpy with the following results:

All the results are of the same format, and they can be summarized in a single equation as

where y is u, u, or h. The subscript “av’’ (for “average’’) is usually dropped for simplicity. The values of the average properties of the mixtures are always between the values of the saturated liquid and the saturated vapor properties (Fig. 3–37). That is,

Finally, all the saturated-mixture states are located under the saturation curve, and to analyze saturated mixtures, all we need are saturated liquid and satu- rated vapor data (Tables A–4 and A–5 in the case of water).

Property tables are also available for saturated solid–vapor mixtures. Properties of saturated ice–water vapor mixtures, for example, are listed in Table A–8. Saturated solid–vapor mixtures can be handled just as saturated liquid– vapor mixtures.

2 Superheated Vapor

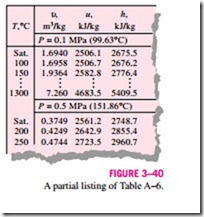
In the region to the right of the saturated vapor line and at temperatures above the critical point temperature, a substance exists as superheated vapor. Since the superheated region is a single-phase region (vapor phase only), temperature and pressure are no longer dependent properties and they can conveniently be used as the two independent properties in the tables. The format of the superheated vapor tables is illustrated in Fig. 3–40.

In these tables, the properties are listed against temperature for selected pressures starting with the saturated vapor data. The saturation temperature is given in parentheses following the pressure value.

Superheated vapor is characterized by

3 Compressed Liquid

Compressed liquid tables are not commonly available, and Table A–7 is the only compressed liquid table in this text. The format of Table A–7 is very much like the format of the superheated vapor tables. One reason for the lack of compressed liquid data is the relative independence of compressed liquid properties from pressure. Variation of properties of compressed liquid with pressure is very mild. Increasing the pressure 100 times often causes proper- ties to change less than 1 percent.

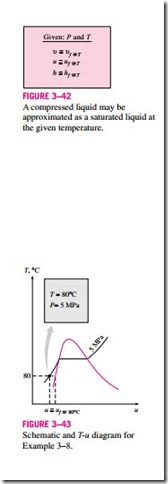
In the absence of compressed liquid data, a general approximation is to treat compressed liquid as saturated liquid at the given temperature (Fig. 3–42). This is because the compressed liquid properties depend on temperature much more strongly than they do on pressure. Thus,

for compressed liquids, where y is u, u, or h. Of these three properties, the property whose value is most sensitive to variations in the pressure is the enthalpy h. Although the above approximation results in negligible error in u and u, the error in h may reach undesirable levels. However, the error in h at very high pressures can be reduced significantly by evaluating it from

Reference State and Reference Values

The values of u, h, and s cannot be measured directly, and they are calculated from measurable properties using the relations between thermodynamic properties. However, those relations give the changes in properties, not the values of properties at specified states. Therefore, we need to choose a convenient reference state and assign a value of zero for a convenient property or proper- ties at that state. For water, the state of saturated liquid at 0.01°C is taken as the reference state, and the internal energy and entropy are assigned zero values at that state. For refrigerant-134a, the state of saturated liquid at -40°C is taken as the reference state, and the enthalpy and entropy are assigned zero values at that state. Note that some properties may have negative values as a result of the reference state chosen.

It should be mentioned that sometimes different tables list different values for some properties at the same state as a result of using a different reference state. However, in thermodynamics we are concerned with the changes in properties, and the reference state chosen is of no consequence in calculations as long as we use values from a single consistent set of tables or charts.