■ VISCOSITY
When two solid bodies in contact move relative to each other, a friction force develops at the contact surface in the direction opposite to motion. To move a table on the floor, for example, we have to apply a force to the table in the horizontal direction large enough to overcome the friction force. The magnitude of the force needed to move the table depends on the friction coefficient between the table and the floor.
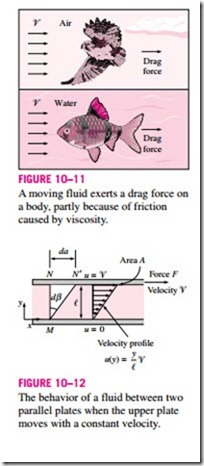
The situation is similar when a fluid moves relative to a solid, or when two fluids move relative to each other. We move with relative ease in air, but not so in water. Moving in oil would be even more difficult, as can be observed by the slower downward motion of a glass ball dropped in a tube filled with oil. It appears that there is a property that represents the internal resistance of a fluid to motion or the “fluidity,” and that property is the viscosity. The force a flowing fluid exerts on a body in the flow direction is called the drag force, and the magnitude of this force depends, in part, on viscosity (Fig. 10–11). To obtain a relation for viscosity, consider a fluid layer between two very large parallel plates (or equivalently, two parallel plates immersed in a large body of a fluid) separated by a distance t’ (Fig. 10–12). Now a constant parallel force F is applied to the upper plate while the lower plate is held fixed.
After the initial transients, it is observed that the upper plate moves continuously under the influence of this force at a constant velocity ‘V. The fluid in contact with the upper plate sticks to the plate surface and moves with it at the same velocity, and the shear stress t acting on this fluid layer is
where A is the contact area between the plate and the fluid. Note that the fluid layer deforms continuously under the influence of shear stress, as expected. The fluid in contact with the lower plate assumes the velocity of that plate, which is zero (again because of the no-slip condition). In steady operation, the fluid velocity between the plates in most cases varies linearly between 0 and ‘V, and thus the velocity profile and the velocity gradient are
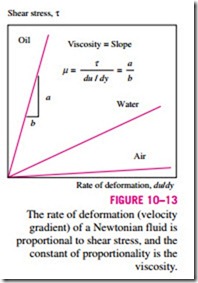
Fluids for which the rate of deformation is proportional to the shear stress are called Newtonian fluids after Sir Isaac Newton, who expressed it first in 1687. Most common fluids such as water, air, gasoline, and oils are Newton- ian fluids. Blood and liquid plastics are examples of non-Newtonian fluids. In one-dimensional flow of Newtonian fluids, shear stress can be expressed
where the constant of proportionality m is called the dynamic (or absolute) viscosity of the fluid, whose unit is kg/m · s, or equivalently, N · s/m2 (or Pa · s where Pa is the pressure unit pascal). A common viscosity unit is poise, which is equivalent to 0.1 Pa · s (or centipoise, which is one-hundredth of a poise). A plot of shear stress versus the rate of deformation (velocity gradient) for a Newtonian fluid is a straight line whose slope is the viscosity of the fluid, as shown in Fig. 10–13. Note that viscosity is independent of the rate of deformation.
The shear force acting on a Newtonian fluid layer (or, by Newton’s third law, the force acting on the plate) is
where again A is the contact area between the plate and the fluid. Then the force F required to move the upper plate in Fig. 10–12 at a constant velocity of ‘V while the lower plate remains stationary is
This relation can alternately be used to calculate m when the force F is measured. Therefore, the experimental setup just described can be used to measure the viscosity of fluids. Note that under identical conditions, the force F will be very different for different fluids.
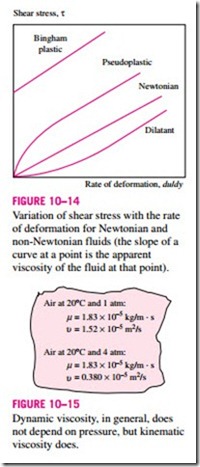
For non-Newtonian fluids, the relationship between shear stress and rate of deformation is not linear, as shown in Fig. 10–14. The slope of the curve on the t versus. du/dy chart is referred to as the apparent viscosity of the fluid. Fluids for which the apparent viscosity increases with the rate of deformation (such as solutions with suspended starch or sand) are referred to as dilatant or shear thickening fluids, and those that exhibit the opposite behavior (the fluid becoming less viscous as it is sheared harder, such as some paints, polymer solutions, and fluids with suspended particles) are referred to as pseudoplastic or shear thinning fluids. Some materials such as toothpaste can resist a finite shear stress and thus behave as a solid, but deform continuously when the shear stress exceeds the yield stress and thus behave as a fluid. Such materials are referred to as bingham plastic.
In fluid mechanics and heat transfer, the ratio of dynamic viscosity to density appears frequently. For convenience, this ratio is given the name kinematic viscosity υ and is expressed as υ = m/r. Two common units of kinematic viscosity are m2/s and stoke (1 stoke = 1 cm2/s = 0.0001 m2/s).
Variation of shear stress with the rate of deformation for Newtonian and non-Newtonian fluids (the slope of a curve at a point is the apparent viscosity of the fluid at that point).
In general, the viscosity of a fluid depends on both temperature and pressure, although the dependence on pressure is rather weak. For liquids, both the dynamic and kinematic viscosities are practically independent of pressure, and any small variation with pressure is usually disregarded, except at extremely high pressures. For gases, this is also the case for dynamic viscosity (at low to moderate pressures), but not for kinematic viscosity since the density of a gas is proportional to its pressure (Fig. 10–15).
The viscosity of a fluid is a measure of its “stickiness” or “resistance to shear.” It is due to the internal frictional force that develops between different layers of fluids as they are forced to move relative to each other. Viscosity is caused by the cohesive forces between the molecules in liquids, and by the molecular collisions in gases, and it varies greatly with temperature. The viscosity of liquids decreases with temperature, whereas the viscosity of gases increases with temperature (Fig. 10–16). This is because in a liquid the mole- cules possess more energy at higher temperatures, and they can oppose the large cohesive intermolecular forces more strongly. As a result, the energized liquid molecules can move more freely.
In a gas, on the other hand, the intermolecular forces are negligible, and the gas molecules at high temperatures move randomly at higher velocities. This results in more molecular collisions per unit volume per unit time, and there- fore in greater resistance to flow. The viscosity of a fluid is directly related to power needed to transport a fluid in a pipe or to move a body (such as a car in air or a submarine in the sea) through a fluid.
The kinetic theory of gases predicts the viscosity of gases to be proportional to the square root of temperature. That is, mgas cc 2T. This prediction is confirmed by practical observations, but deviations for different gases need to be accounted for by incorporating some correction factors. The viscosity of gases is given as a function of temperature by the Sutherland correlation (from The U.S. Standard Atmosphere) as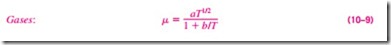
where T is absolute temperature, and a and b are experimentally determined constants. Note that measuring viscosities at two different temperatures is suf- ficient to determine these constants. For air, the values of these constants are a = 1.458 X 10-6 kg/(m · s · K1/2) and b = 110.4 K at atmospheric conditions. The viscosity of gases is independent of pressure at low to moderate pressures (from a few percent of 1 atm to several atm). But viscosity increases at high pressures due to the increase in density.
For liquids, the viscosity is given as
where L is the length of the cylinder and n· is the number of revolutions per unit time, which is usually expressed in rpm (revolutions per minute). Note that the angular distance traveled during one rotation is 2p radians, and thus the relation between the angular velocity in rad/min and the rpm is v = 2pn·.
Equation 10–11 can be used to calculate the viscosity of a fluid by measuring torque at a specified angular velocity. Therefore, two concentric cylinders can be used as a viscometer, a device that measures viscosity.
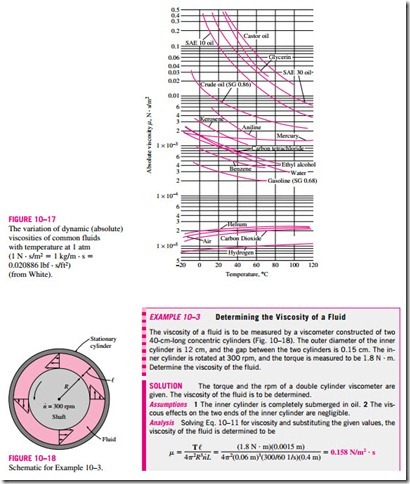
The viscosities of some fluids at room temperature are listed in Table 10–2. They are plotted against the temperature in Fig. 10–17. Note that the viscosities of different fluids differ by several orders of magnitude. Also note that it is more difficult to move an object in a higher-viscosity fluid such as engine oil than it is in a lower-viscosity fluid such as water. Liquids, in general, are much more viscous than gases.