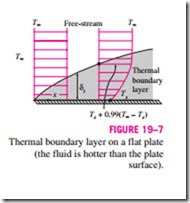
THERMAL BOUNDARY LAYER
We have seen in Chap. 15 that a velocity boundary layer develops when a fluid flows over a surface as a result of the fluid layer adjacent to the surface assuming the surface velocity (i.e., zero velocity relative to the surface). Also, we defined the velocity boundary layer as the region in which the fluid velocity varies from zero to 0.99V. Likewise, a thermal boundary layer develops when a fluid at a specified temperature flows over a surface that is at a different temperature, as shown in Fig. 19–7.
Consider the flow of a fluid at a uniform temperature of Too over an isothermal flat plate at temperature Ts. The fluid particles in the layer adjacent to the surface will reach thermal equilibrium with the plate and assume the surface temperature Ts. These fluid particles will then exchange energy with the paticles in the adjoining-fluid layer, and so on. As a result, a temperature profile will develop in the flow field that ranges from Ts at the surface to Too sufficiently far from the surface. The flow region over the surface in which the temperature variation in the direction normal to the surface is significant is the thermal boundary layer. The thickness of the thermal boundary layer dt at any location along the surface is defined as the distance from the surface at which the temperature difference T – Ts equals 0.99(Too – Ts). Note that for the special case of Ts = 0, we have T = 0.99Too at the outer edge of the ther- mal boundary layer, which is analogous to u = 0.99V for the velocity boundary layer.
The thickness of the thermal boundary layer increases in the flow direction, since the effects of heat transfer are felt at greater distances from the surface further downstream.
The convection heat transfer rate anywhere along the surface is directly related to the temperature gradient at that location. Therefore, the shape of the temperature profile in the thermal boundary layer dictates the convection heat transfer between a solid surface and the fluid flowing over it. In flow over a heated (or cooled) surface, both velocity and thermal boundary layers will develop simultaneously. Noting that the fluid velocity will have a strong influence on the temperature profile, the development of the velocity boundary layer relative to the thermal boundary layer will have a strong effect on the convection heat transfer.
Prandtl Number
The relative thickness of the velocity and the thermal boundary layers is best described by the dimensionless parameter Prandtl number, defined as
It is named after Ludwig Prandtl, who introduced the concept of boundary layer in 1904 and made significant contributions to boundary layer theory.
The Prandtl numbers of fluids range from less than 0.01 for liquid metals to more than 100,000 for heavy oils (Table 19–1). Note that the Prandtl number is in the order of 10 for water.
The Prandtl numbers of gases are about 1, which indicates that both momentum and heat dissipate through the fluid at about the same rate. Heat diffuses very quickly in liquid metals (Pr � 1) and very slowly in oils (Pr � 1) relative to momentum. Consequently the thermal boundary layer is much thicker for liquid metals and much thinner for oils relative to the velocity boundary layer.