INTRODUCTION TO FLUID MECHANICS:SURFACE TENSION AND CAPILLARY EFFECT

SURFACE TENSION AND CAPILLARY EFFECT

It is often observed that a drop of blood forms a hump on a horizontal glass, a drop of mercury forms a near-perfect sphere and can be rolled just like a steel ball over a smooth surface; water droplets from rain or dew hang from branches or leaves of trees; a liquid fuel injected into an engine forms a mist of spherical droplets; water dripping from a leaky faucet falls as spherical droplets; and a soap bubble released into the air forms a spherical shape (Fig. 10–19).

In these and other observances, liquid droplets behave like small spherical balloons filled with the liquid, and the surface of the liquid acts like a stretched elastic membrane under tension. The pulling force that causes this tension acts parallel to the surface and is due to the attractive forces between the molecules of the liquid. The magnitude of this force per unit length is called surface tension ss and is usually expressed in the unit N/m (or lbf/ft in English units). This effect is also called surface energy and is expressed in the equivalent unit of N · m/m2 or J/m2. In this case, ss represents the stretching work that needs to be done to increase the surface area of the liquid by a unit amount.

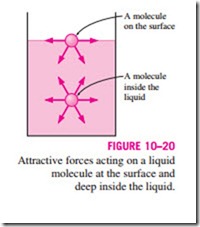
To visualize how surface tension arises, we present a microscopic view in Fig. 10–20 by considering two liquid molecules, one at the surface and one deep within the liquid body. The attractive forces applied on the interior mol- ecule by the surrounding molecules balance each other because of symmetry. But the attractive forces acting on the surface molecule are not symmetric, and the attractive forces applied by the gas molecules above are usually very small. Therefore, there is a net attractive force acting on the molecule at the surface of the liquid, which tends to pull the molecules on the surface toward the interior of the liquid. This force is balanced by the repulsive forces from

the molecules below the surface that are being compressed. The resulting compression effect causes the liquid to minimize its surface area. This is the reason for the tendency of the liquid droplets to attain a spherical shape, which has the minimum surface area for a given volume.

You also may have observed, with amusement, that some insects can land on water (even walk on water) and that small steel needles can float on water. These are again made possible by surface tension that balances the weights of these objects.

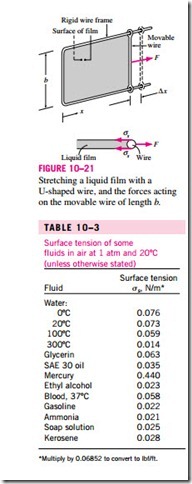
To understand the surface tension effect better, consider a liquid film (such as the film of a soap bubble) suspended on a U-shaped wire frame with a movable side (Fig. 10–21). Normally, the liquid film tends to pull the movable wire inward in order to minimize its surface area. A force F needs to be ap- plied on the movable wire in the opposite direction to balance this pulling effect. The thin film in the device has two surfaces (the top and bottom surfaces) exposed to air, and thus the length along which the tension acts in this case is 2b. Then a force balance on the movable wire gives F = 2bss, and thus the surface tension can be expressed as

Note that for b = 0.5 m, the force F measured (in N) is simply the surface tension in N/m. An apparatus of this kind with sufficient precision can be used In the U-shaped wire, the force F remains constant as the movable wire is pulled to stretch the film and increase its surface area. When the movable wire is pulled a distance dx, the surface area increases by dA = 2b dx, and the work done W during this stretching process is

since the force remains constant in this case. This result can also be interpreted as the surface energy of the film is increased by an amount ss dA during this stretching process, which is consistent with the alternative interpretation of ss as surface energy. This is similar to a rubber band having more temperature for a given substance, as shown in Table 10–3. At 20°C, for ex- ample, the surface tension is 0.073 N/m for water and 0.440 N/m for mercury surrounded by atmospheric air. The very high surface tension also explains why mercury droplets form spherical balls that can be rolled like a solid ball on a surface without wetting the surface. The surface tension of a liquid, in general, decreases with temperature and becomes zero at the critical point (and thus there is no distinct liquid–vapor interface at temperatures above the *Multiply by 0.06852 to convert to lbf/ft.

critical point). The effect of pressure on surface tension is usually negligible.

The surface tension of a substance can be changed considerably by impurities. Therefore, certain chemicals, called surfactants, can be added to a liquid to decrease its surface tension. For example, soaps and detergents lower the surface tension of water and enable it to penetrate through the small openings between fibers for more effective washing. But this also means that devices whose operation depends on surface tension (such as heat pipes) can be destroyed by the presence of impurities due to poor workmanship.

We speak of surface tension for liquids only at liquid–liquid or liquid–gas interfaces. Therefore, it is important to specify the adjacent liquid or gas when specifying surface tension. Also, surface tension determines the size of the liquid droplets that form. A droplet that keeps growing by the addition of more mass will break down when the surface tension can no longer hold it together. This is like a balloon that will burst while being inflated when the pressure in- side rises above the strength of the balloon material.

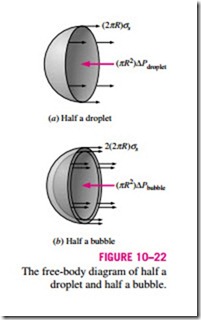
A curved interface indicates a pressure difference (or “pressure jump”) across the interface with pressure being higher on the concave side. The excess pressure dP inside a droplet or bubble above the atmospheric pressure, for example, can be determined by considering the free-body diagram of half a droplet or bubble (Fig. 10–22). Noting that surface tension acts along the circumference and the pressure acts on the area, horizontal force balances for the droplet and the bubble give

where Pi and Po are the pressures inside and outside the droplet or bubble, respectively. When the droplet or bubble is in the atmosphere, Po is simply atmospheric pressure. The factor 2 in the force balance for the bubble is due to the bubble consisting of a film with two surfaces (inner and outer surfaces) and thus two circumferences in the cross section.

The excess pressure in a droplet (or bubble) also can be determined by considering a differential increase in the radius of the droplet due to the addition of a differential amount of mass and interpreting the surface tension as the increase in the surface energy per unit area. Then the increase in the surface energy of the droplet during this differential expansion process becomes

Equating the two expressions above gives dPdroplet = 2ss /R, which is the same relation obtained before and given in Eq. 10–13. Note that the excess pressure in a droplet or bubble is inversely proportional to the radius.

Capillary Effect

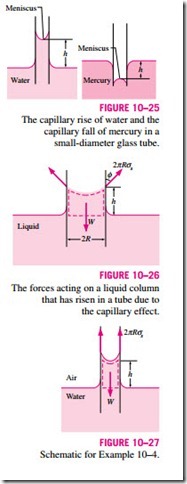
Another interesting consequence of surface tension is the capillary effect, which is the rise or fall of a liquid in a small-diameter tube inserted into the liquid. Such narrow tubes or confined flow channels are called capillaries. The rise of kerosene through a cotton wick inserted into the reservoir of a kerosene lamp is due to this effect. The capillary effect is also partially responsible for the rise of water to the top of tall trees. The curved free surface of a liquid in a capillary tube is called the meniscus.

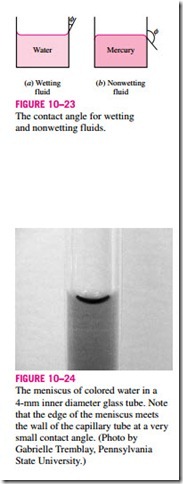
It is commonly observed that water in a glass container curves up slightly at the edges where it touches the glass surface; but the opposite occurs for mercury: it curves down at the edges (Fig. 10–23). This effect is usually expressed by saying that water wets the glass (by sticking to it) while mercury does not. The strength of the capillary effect is quantified by the contact (or wetting) angle f, defined as the angle that the tangent to the liquid surface makes with the solid surface at the point of contact. The surface tension force acts along this tangent line toward the solid surface. A liquid is said to wet the surface when f < 90º and not to wet the surface when f > 90º. In atmospheric air, the contact angle of water (and most other organic liquids) with glass is nearly

zero, f = 0º (Fig. 10–24). Therefore, the surface tension force acts upward on water in a glass tube along the circumference, tending to pull the water up. As a result, water rises in the tube until the weight of the liquid in the tube above the liquid level of the reservoir balances the surface tension force. The contact angle is 130º for mercury–glass and 26º for kerosene–glass in air. Note that the contact angle, in general, is different in different environments (such as another gas or liquid in place of air).

The phenomenon of capillary effect can be explained microscopically by considering cohesive forces (the forces between like molecules, like water) and adhesive forces (the forces between dislike molecules, like water and glass). The liquid molecules at the solid–liquid interface are subjected to both cohesive forces by other liquid molecules and adhesive forces by the molecules of the solid. The relative magnitudes of these forces determine whether a liquid wets a solid surface or not. Obviously, the water molecules are more strongly attracted to the glass molecules than they are to other water molecules, and thus water tends to rise along the glass surface. The opposite occurs for mercury, which causes the liquid surface near the glass wall to be sup- pressed (Fig. 10–25).

The magnitude of the capillary rise in a circular tube can be determined from a force balance on the cylindrical liquid column of height h in the tube (Fig. 10–26). The bottom of the liquid column is at the same level as the free surface of the reservoir, and thus the pressure there must be atmospheric pressure. This balances the atmospheric pressure acting at the top surface, and thus these two effects cancel each other. The weight of the liquid column is approximately

This relation is also valid for nonwetting liquids (such as mercury in glass) and gives the capillary drop. In this case f > 90º and thus cos f < 0, which makes h negative. Therefore, a negative value of capillary rise corresponds to a capillary drop (Fig. 10–25).

Note that the capillary rise is inversely proportional to the radius of the tube. Therefore, the thinner the tube is, the greater the rise (or fall) of the liquid in the tube. In practice, the capillary effect is usually negligible in tubes whose diameter is greater than 1 cm. When pressure measurements are made using manometers and barometers, it is important to use sufficiently large tubes to minimize the capillary effect. The capillary rise is also inversely proportional to the density of the liquid, as expected. Therefore, lighter liquids experience greater capillary rises. Finally, it should be kept in mind that Eq. 10–15 is de- rived for constant diameter tubes and should not be used for tubes of variable cross section.