EQUATION OF MOTION AND THE GRASHOF NUMBER
In this section we derive the equation of motion that governs the natural convection flow in laminar boundary layer. The conservation of mass and energy equations derived in Chap. 6 for forced convection are also applicable for natural convection, but the momentum equation needs to be modified to incorporate buoyancy.
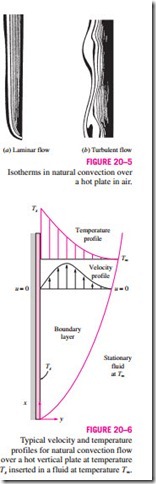
Consider a vertical hot flat plate immersed in a quiescent fluid body. We assume the natural convection flow to be steady, laminar, and two-dimensional, and the fluid to be Newtonian with constant properties, including density, with one exception: the density difference rroo is to be considered since it is this density difference between the inside and the outside of the boundary layer that gives rise to buoyancy force and sustains flow. (This is known as the Boussinesq approximation.) We take the upward direction along the plate to be x, and the direction normal to surface to be y, as shown in Fig. 20–6. There- fore, gravity acts in the –x-direction. Noting that the flow is steady and two-
dimensional, the x– and y-components of velocity within boundary layer are u = u(x, y) and υ = υ(x, y), respectively.
The velocity and temperature profiles for natural convection over a vertical hot plate are also shown in Fig. 20–6. Note that as in forced convection, the thickness of the boundary layer increases in the flow direction. Unlike forced convection, however, the fluid velocity is zero at the outer edge of the velocity boundary layer as well as at the surface of the plate. This is expected since the fluid beyond the boundary layer is motionless. Thus, the fluid velocity in- creases with distance from the surface, reaches a maximum, and gradually de- creases to zero at a distance sufficiently far from the surface. At the surface, the fluid temperature is equal to the plate temperature, and gradually de- creases to the temperature of the surrounding fluid at a distance sufficiently far from the surface, as shown in the figure. In the case of cold surfaces, the shape of the velocity and temperature profiles remains the same but their direction is reversed.
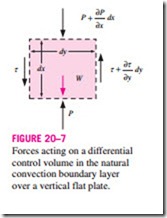
Consider a differential volume element of height dx, length dy, and unit depth in the z-direction (normal to the paper) for analysis. The forces acting on this volume element are shown in Fig. 20–7. Newton’s second law of motion for this control volume can be expressed as Typical velocity and temperature profiles for natural convection flow over a hot vertical plate at temperature Ts inserted in a fluid at temperature Too.
 The forces acting on the differential volume element in the vertical direction are the pressure forces acting on the top and bottom surfaces, the shear stresses acting on the side surfaces (the normal stresses acting on the top and bottom surfaces are small and are disregarded), and the force of gravity acting on the entire volume element. Then the net surface force acting in the x-direction becomes
The forces acting on the differential volume element in the vertical direction are the pressure forces acting on the top and bottom surfaces, the shear stresses acting on the side surfaces (the normal stresses acting on the top and bottom surfaces are small and are disregarded), and the force of gravity acting on the entire volume element. Then the net surface force acting in the x-direction becomes
which is simply the relation for the variation of hydrostatic pressure in a quiescent fluid with height, as expected. Also, noting that υ � u in the boundary layer and thus aυ/ax = aυ/ay = 0, and that there are no body forces (including gravity) in the y-direction, the force balance in that direction gives aP/ay = 0. That is, the variation of pressure in the direction normal to the surface is negligible, and for a given x the pressure in the boundary layer is equal to the pressure in the quiescent fluid. Therefore, P = P(x) = Poo(x) and aP/ax = aPoo/ax = -roog. Substituting into Eq. 20–10,
The last term represents the net upward force per unit volume of the fluid (the difference between the buoyant force and the fluid weight). This is the force that initiates and sustains convection currents.
From Eq. 20–5, we have roo – r = rb(T – Too). Substituting it into the last equation and dividing both sides by r gives the desired form of the x-momentum equation,
This is the equation that governs the fluid motion in the boundary layer due to the effect of buoyancy. Note that the momentum equation involves the temperature, and thus the momentum and energy equations must be solved simultaneously.
The set of three partial differential equations (the continuity, momentum, and the energy equations) that govern natural convection flow over vertical isothermal plates can be reduced to a set of two ordinary nonlinear differential equations by the introduction of a similarity variable. But the resulting equations must still be solved numerically [Ostrach (1953)]. Interested readers are referred to advanced books on the topic for detailed discussions [e.g., Kays and Crawford (1993)].
The Grashof Number
The governing equations of natural convection and the boundary conditions can be nondimensionalized by dividing all dependent and independent variables by suitable constant quantities: all lengths by a characteristic length Lc , all velocities by an arbitrary reference velocity ‘V (which, from the definition of Reynolds number, is taken to be ‘V = ReL υ/Lc), and temperature by a suit- able temperature difference (which is taken to be Ts – Too) as
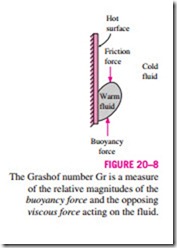
We mentioned in the preceding chapters that the flow regime in forced convection is governed by the dimensionless Reynolds number, which represents the ratio of inertial forces to viscous forces acting on the fluid. The flow regime in natural convection is governed by the dimensionless Grashof number, which represents the ratio of the buoyancy force to the viscous force acting on the fluid (Fig. 20–8).
The role played by the Reynolds number in forced convection is played by the Grashof number in natural convection. As such, the Grashof number pro- vides the main criterion in determining whether the fluid flow is laminar or turbulent in natural convection. For vertical plates, for example, the critical Grashof number is observed to be about 10 9. Therefore, the flow regime on a vertical plate becomes turbulent at Grashof numbers greater than 109.
When a surface is subjected to external flow, the problem involves both natural and forced convection. The relative importance of each mode of heat transfer is determined by the value of the coefficient GrL /Re 2: Natural con- vection effects are negligible if GrL /ReL � 1, free convection dominates and the forced convection effects are negligible if GrL/ReL are significant and must be considered if GrL /Re 2
Incoming search terms:
- Girsohf equation
- grashof number
- grashof number example
- modified reynolds equation convection
- convection equation of motion
- equation of motion for natural convection
- equation of motion in convection
- formula of grashoff number
- velocity & temperature profile for natural convention for cold surface