■ NATURAL CONVECTION OVER SURFACES
Natural convection heat transfer on a surface depends on the geometry of the surface as well as its orientation. It also depends on the variation of temperature on the surface and the thermophysical properties of the fluid involved. Although we understand the mechanism of natural convection well, the complexities of fluid motion make it very difficult to obtain simple analytical relations for heat transfer by solving the governing equations of motion and energy. Some analytical solutions exist for natural convection, but such solutions lack generality since they are obtained for simple geometries under some simplifying assumptions. Therefore, with the exception of some simple cases, heat transfer relations in natural convection are based on experimental studies. Of the numerous such correlations of varying complexity and claimed accuracy available in the literature for any given geometry, we present here the ones that are best known and widely used.
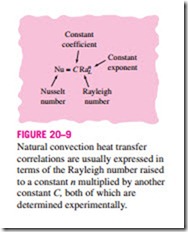
The simple empirical correlations for the average Nusselt number Nu in natural convection are of the form (Fig. 20–9)
The values of the constants C and n depend on the geometry of the surface and the flow regime, which is characterized by the range of the Rayleigh number. The value of n is usually 1 for laminar flow and 1 for turbulent flow. The value of the constant C is normally less than 1.
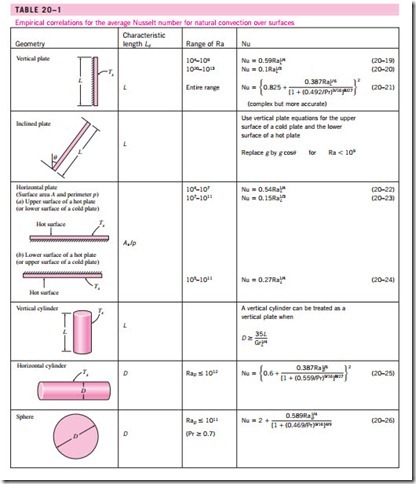
![clip_image007[1] clip_image007[1]](http://machineryequipmentonline.com/hydraulics-and-pneumatics/wp-content/uploads/2016/03/clip_image0071_thumb.gif) Simple relations for the average Nusselt number for various geometries are given in Table 20–1, together with sketches of the geometries. Also given in this table are the characteristic lengths of the geometries and the ranges of Rayleigh number in which the relation is applicable. All fluid properties are to be evaluated at the film temperature Tf = 1(Ts + Too).
Simple relations for the average Nusselt number for various geometries are given in Table 20–1, together with sketches of the geometries. Also given in this table are the characteristic lengths of the geometries and the ranges of Rayleigh number in which the relation is applicable. All fluid properties are to be evaluated at the film temperature Tf = 1(Ts + Too).
When the average Nusselt number and thus the average convection coef- ficient is known, the rate of heat transfer by natural convection from a solid surface at a uniform temperature Ts to the surrounding fluid is expressed by Newton’s law of cooling as
where As is the heat transfer surface area and h is the average heat transfer co- efficient on the surface.
Vertical Plates (Ts = constant)
For a vertical flat plate, the characteristic length is the plate height L. In Table20–1 we give three relations for the average Nusselt number for an isothermal vertical plate. The first two relations are very simple. Despite its complexity, we suggest using the third one (Eq. 20–21) recommended by Churchill and Chu (1975) since it is applicable over the entire range of Rayleigh number.
This relation is most accurate in the range of 10-1 < Ra
Vertical Plates (q˙ s = constant)
In the case of constant surface heat flux, the rate of heat transfer is known (it is simply Q = qs A s ), but the surface temperature Ts is not. In fact, Ts in- creases with height along the plate. It turns out that the Nusselt number rela- tions for the constant surface temperature and constant surface heat flux cases are nearly identical [Churchill and Chu (1975)]. Therefore, the relations for isothermal plates can also be used for plates subjected to uniform heat flux, provided that the plate midpoint temperature TL /2 is used for Ts in the evaluation of the film temperature, Rayleigh number, and the Nusselt number. Noting that h = · / (T – T ), the average Nusselt number in this case can be expressed as
The midpoint temperature TL /2 is determined by iteration so that the Nusselt numbers determined from Eqs. 20–21 and 20–19 match.
Vertical Cylinders
An outer surface of a vertical cylinder can be treated as a vertical plate when
the diameter of the cylinder is sufficiently large so that the curvature effects are negligible. This condition is satisfied if
When this criteria is met, the relations for vertical plates can also be used for y vertical cylinders. Nusselt number relations for slender cylinders that do not meet this criteria are available in the literature [e.g., Cebeci (1974)].
Inclined Plates
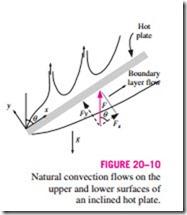
Consider an inclined hot plate that makes an angle u from the vertical, as shown in Fig. 20–10, in a cooler environment. The net force F = g(roo – r) (the difference between the buoyancy and gravity) acting on a unit volume of the fluid in the boundary layer is always in the vertical direction. In the case
of inclined plate, this force can be resolved into two components: Fy = F cos u parallel to the plate that drives the flow along the plate, and Fy = F sin u nor- mal to the plate. Noting that the force that drives the motion is reduced, we expect the convection currents to be weaker, and the rate of heat transfer to be lower relative to the vertical plate case.
The experiments confirm what we suspect for the lower surface of a hot plate, but the opposite is observed on the upper surface. The reason for this curious behavior for the upper surface is that the force component Fy initiates upward motion in addition to the parallel motion along the plate, and thus the boundary layer breaks up and forms plumes, as shown in the figure. As a result, the thickness of the boundary layer and thus the resistance to heat trans- fer decreases, and the rate of heat transfer increases relative to the vertical orientation.
In the case of a cold plate in a warmer environment, the opposite occurs as expected: The boundary layer on the upper surface remains intact with weaker boundary layer flow and thus lower rate of heat transfer, and the boundary layer on the lower surface breaks apart (the colder fluid falls down) and thus enhances heat transfer.
When the boundary layer remains intact (the lower surface of a hot plate or the upper surface of a cold plate), the Nusselt number can be determined from the vertical plate relations provided that g in the Rayleigh number relation is replaced by g cos u for u < 60°. Nusselt number relations for the other two surfaces (the upper surface of a hot plate or the lower surface of a cold plate) are available in the literature [e.g., Fujiii and Imura (1972)].
Horizontal Plates
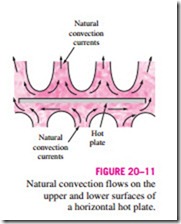
The rate of heat transfer to or from a horizontal surface depends on whether the surface is facing upward or downward. For a hot surface in a cooler environment, the net force acts upward, forcing the heated fluid to rise. If the hot surface is facing upward, the heated fluid rises freely, inducing strong natural convection currents and thus effective heat transfer, as shown in Fig. 20–11. But if the hot surface is facing downward, the plate will block the heated fluid that tends to rise (except near the edges), impeding heat transfer. The opposite is true for a cold plate in a warmer environment since the net force (weight minus buoyancy force) in this case acts downward, and the cooled fluid near the plate tends to descend.
The average Nusselt number for horizontal surfaces can be determined from
where As is the surface area and p is the perimeter. Note that Lc = a/4 for a horizontal square surface of length a, and D/4 for a horizontal circular surface of diameter D.
Horizontal Cylinders and Spheres
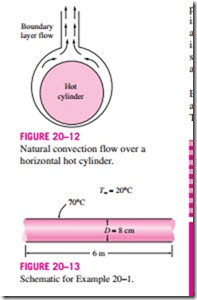
The boundary layer over a hot horizontal cylinder starts to develop at the bottom, increasing in thickness along the circumference, and forming a rising
plume at the top, as shown in Fig. 20–12. Therefore, the local Nusselt number is highest at the bottom, and lowest at the top of the cylinder when the boundary layer flow remains laminar. The opposite is true in the case of a cold horizontal cylinder in a warmer medium, and the boundary layer in this case starts to develop at the top of the cylinder and ending with a descending plume at the bottom.
Incoming search terms:
- cylinder cylinder free convection
- natural convection over surfaces
- nusselt number characteristic length
- parallel plate constant heat flux heat transfer
- vertical Plate surface area formula