PROPERTIES OF PURE SUBSTANCES:PROPERTY DIAGRAMS FOR PHASE-CHANGE PROCESSES

PROPERTY DIAGRAMS FOR PHASE-CHANGE PROCESSES

The variations of properties during phase-change processes are best studied and understood with the help of property diagrams. Next, we develop and dis- cuss the T–u, P–u, and P-T diagrams for pure substances.

1 The T-v Diagram

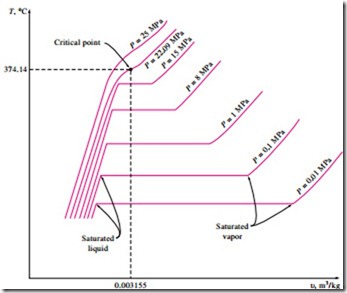
The phase-change process of water at 1 atm pressure was described in detail in the last section and plotted on a T–u diagram in Fig. 3–11. Now we repeat this process at different pressures to develop the T–u diagram.

Let us add weights on top of the piston until the pressure inside the cylinder reaches 1 MPa. At this pressure, water will have a somewhat smaller specific volume than it did at 1 atm pressure. As heat is transferred to the water at this new pressure, the process will follow a path that looks very much like the process path at 1 atm pressure, as shown in Fig. 3–16, but there are some noticeable differences. First, water will start boiling at a much higher temper- ature (179.9°C) at this pressure. Second, the specific volume of the saturated liquid is larger and the specific volume of the saturated vapor is smaller than the corresponding values at 1 atm pressure. That is, the horizontal line that connects the saturated liquid and saturated vapor states is much shorter.

As the pressure is increased further, this saturation line will continue to get shorter, as shown in Fig. 3–16, and it will become a point when the pressure reaches 22.09 MPa for the case of water. This point is called the critical point, and it is defined as the point at which the saturated liquid and saturated vapor states are identical.

The temperature, pressure, and specific volume of a substance at the critical point are called, respectively, the critical temperature Tcr, critical pressure Pcr, and critical specific volume ucr. The critical-point properties of water are Pcr

= 22.09 MPa, Tcr = 374.14°C, and ucr = 0.003155 m3/kg. For helium, they are 0.23 MPa, -267.85°C, and 0.01444 m3/kg. The critical properties for var- ious substances are given in Table A–1 in the appendix.

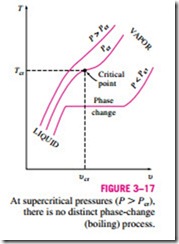
At pressures above the critical pressure, there will not be a distinct phase- change process (Fig. 3–17). Instead, the specific volume of the substance will continually increase, and at all times there will be only one phase present. Eventually, it will resemble a vapor, but we can never tell when the change

has occurred. Above the critical state, there is no line that separates the com- pressed liquid region and the superheated vapor region. However, it is customary to refer to the substance as superheated vapor at temperatures above the critical temperature and as compressed liquid at temperatures below the critical temperature.

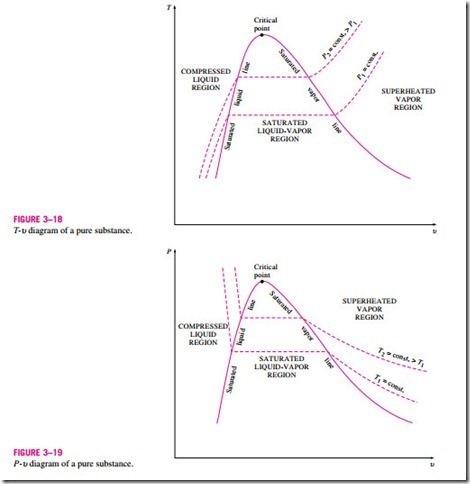
The saturated liquid states in Fig. 3–16 can be connected by a line called the saturated liquid line, and saturated vapor states in the same figure can be connected by another line, called the saturated vapor line. These two lines meet at the critical point, forming a dome as shown in Fig. 3–18. All the com- pressed liquid states are located in the region to the left of the saturated liquid line, called the compressed liquid region. All the superheated vapor states are located to the right of the saturated vapor line, called the superheated vapor region. In these two regions, the substance exists in a single phase, a liquid or a vapor. All the states that involve both phases in equilibrium are located under the dome, called the saturated liquid–vapor mixture region, or the wet region.

2 The P-v Diagram

The general shape of the P-u diagram of a pure substance is very much like the T–u diagram, but the T = constant lines on this diagram have a downward trend, as shown in Fig. 3–19.

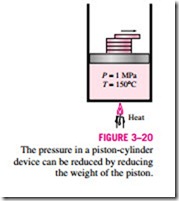
Consider again a piston-cylinder device that contains liquid water at 1 MPa and 150°C. Water at this state exists as a compressed liquid. Now the weights on top of the piston are removed one by one so that the pressure inside the cylinder decreases gradually (Fig. 3–20). The water is allowed to exchange

heat with the surroundings so its temperature remains constant. As the pressure decreases, the volume of the water will increase slightly. When the pressure reaches the saturation-pressure value at the specified temperature (0.4758 MPa), the water will start to boil. During this vaporization process, both the temperature and the pressure remain constant, but the specific volume in- creases. Once the last drop of liquid is vaporized, further reduction in pressure results in a further increase in specific volume. Notice that during the phase- change process, we did not remove any weights. Doing so would cause the pressure and therefore the temperature to drop [since Tsat = f (Psat)], and the process would no longer be isothermal.

If the process is repeated for other temperatures, similar paths will be obtained for the phase-change processes. Connecting the saturated liquid and the saturated vapor states by a curve, we obtain the P-u diagram of a pure sub- stance, as shown in Fig. 3–19.

Extending the Diagrams to Include the Solid Phase

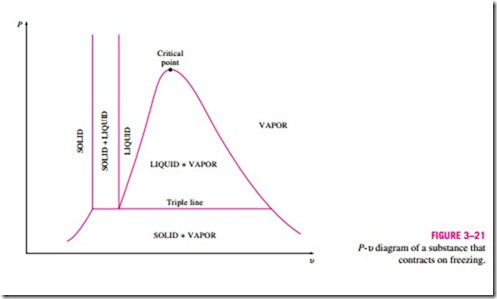
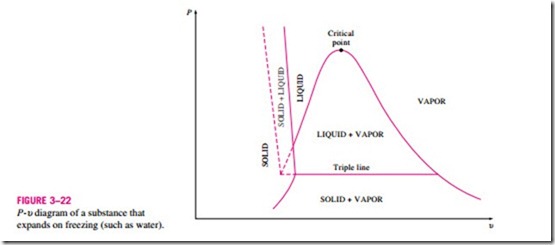
The two equilibrium diagrams developed so far represent the equilibrium states involving the liquid and the vapor phases only. However, these diagrams can easily be extended to include the solid phase as well as the solid–liquid and the solid–vapor saturation regions. The basic principles dis- cussed in conjunction with the liquid–vapor phase-change process apply equally to the solid–liquid and solid–vapor phase-change processes. Most substances contract during a solidification (i.e., freezing) process. Others, like water, expand as they freeze. The P–u diagrams for both groups of substances are given in Figs. 3–21 and 3–22. These two diagrams differ only in the solid–liquid saturation region. The T–u diagrams look very much like the P–u diagrams, especially for substances that contract on freezing.

The fact that water expands upon freezing has vital consequences in nature. If water contracted on freezing as most other substances do, the ice formed would be heavier than the liquid water, and it would settle to the bottom of rivers, lakes, and oceans instead of floating at the top. The sun’s rays would never reach these ice layers, and the bottoms of many rivers, lakes, and oceans would be covered with ice year round, seriously disrupting marine life.

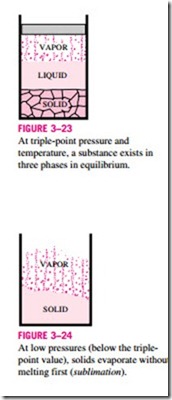
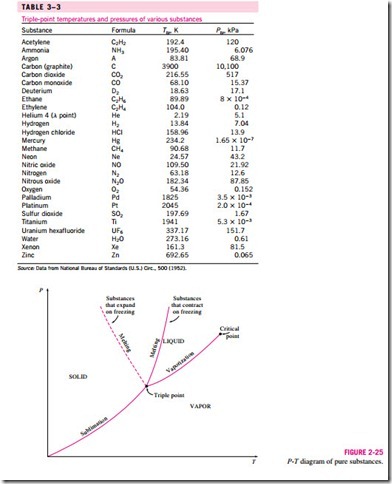
We are all familiar with two phases being in equilibrium, but under some conditions all three phases of a pure substance coexist in equilibrium (Fig. 3–23). On P–u or T–u diagrams, these triple-phase states form a line called the triple line. The states on the triple line of a substance have the same pressure and temperature but different specific volumes. The triple line appears as a point on the P-T diagrams and, therefore, is often called the triple point. The triple-point temperatures and pressures of various substances are given in Table 3–3. For water, the triple-point temperature and pressure are 0.01°C and 0.6113 kPa, respectively. That is, all three phases of water will exist in equi- librium only if the temperature and pressure have precisely these values. No substance can exist in the liquid phase in stable equilibrium at pressures below the triple-point pressure. The same can be said for temperature for substances that contract on freezing. However, substances at high pressures can exist in the liquid phase at temperatures below the triple-point temperature. For ex- ample, water cannot exist in liquid form in equilibrium at atmospheric pressure at temperatures below 0°C, but it can exist as a liquid at -20°C at 200 MPa pressure. Also, ice exists at seven different solid phases at pressures above 100 MPa.

There are two ways a substance can pass from the solid to vapor phase: either it melts first into a liquid and subsequently evaporates, or it evaporates directly without melting first. The latter occurs at pressures below the triple- point value, since a pure substance cannot exist in the liquid phase at those pressures (Fig. 3–24). Passing from the solid phase directly into the vapor phase is called sublimation. For substances that have a triple-point pressure above the atmospheric pressure such as solid CO2 (dry ice), sublimation is the only way to change from the solid to vapor phase at atmospheric conditions.

3 The P-T Diagram

Figure 3–25 shows the P-T diagram of a pure substance. This diagram is often called the phase diagram since all three phases are separated from each other by three lines. The sublimation line separates the solid and vapor regions, the vaporization line separates the liquid and vapor regions, and the melting (or

fusion) line separates the solid and liquid regions. These three lines meet at the triple point, where all three phases coexist in equilibrium. The vaporization line ends at the critical point because no distinction can be made between liquid and vapor phases above the critical point. Substances that expand and contract on freezing differ only in the melting line on the P-T diagram.

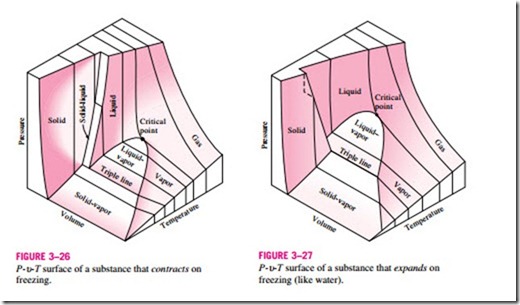
The P-v-T Surface

The state of a simple compressible substance is fixed by any two independent, intensive properties. Once the two appropriate properties are fixed, all the other properties become dependent properties. Remembering that any equation with two independent variables in the form z = z(x, y) represents a surface in space, we can represent the P–u–T behavior of a substance as a surface in space, as shown in Figs. 3–26 and 3–27. Here T and u may be viewed as the independent variables (the base) and P as the dependent variable (the height). All the points on the surface represent equilibrium states. All states along the path of a quasi-equilibrium process lie on the P-u-T surface since such a process must pass through equilibrium states. The single-phase regions appear as curved surfaces on the P-u–T surface, and the two-phase regions as surfaces perpendicular to the P-T plane. This is expected since the projections of two-phase regions on the P-T plane are lines.

All the two-dimensional diagrams we have discussed so far are merely projections of this three-dimensional surface onto the appropriate planes. A P-u diagram is just a projection of the P–u–T surface on the P–u plane, and a T–u diagram is nothing more than the bird’s-eye view of this surface. The P-u–T surfaces present a great deal of information at once, but in a thermo- dynamic analysis it is more convenient to work with two-dimensional diagrams, such as the P–u and T–u diagrams.