The convection heat transfer coefficient is a strong function of velocity: the higher the velocity, the higher the convection heat transfer coefficient. The fluid velocities associated with natural convection are low, typically less than 1 m/s. Therefore, the heat transfer coefficients encountered in natural convection are usually much lower than those encountered in forced convection. Yet several types of heat transfer equipment are designed to operate under natural convection conditions instead of forced convection, because natural convection does not require the use of a fluid mover.
We start this chapter with a discussion of the physical mechanism of natural convection and the Grashof number. We then present the correlations to evaluate heat transfer by natural convection for various geometries, including finned surfaces and enclosures. Finally, we discuss simultaneous forced and natural convection.
■ PHYSICAL MECHANISM OF NATURAL CONVECTION
Many familiar heat transfer applications involve natural convection as the primary mechanism of heat transfer. Some examples are cooling of electronic equipment such as power transistors, TVs, and VCRs; heat transfer from elec- tric baseboard heaters or steam radiators; heat transfer from the refrigeration coils and power transmission lines; and heat transfer from the bodies of animals and human beings. Natural convection in gases is usually accompanied by radiation of comparable magnitude except for low-emissivity surfaces.
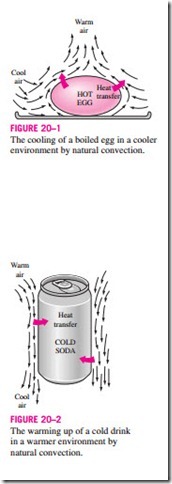
We know that a hot boiled egg (or a hot baked potato) on a plate eventually cools to the surrounding air temperature (Fig. 20–1). The egg is cooled by transferring heat by convection to the air and by radiation to the surrounding surfaces. Disregarding heat transfer by radiation, the physical mechanism of cooling a hot egg (or any hot object) in a cooler environment can be explained as follows:
As soon as the hot egg is exposed to cooler air, the temperature of the outer surface of the egg shell will drop somewhat, and the temperature of the air adjacent to the shell will rise as a result of heat conduction from the shell to the air. Consequently, the egg will soon be surrounded by a thin layer of warmer air, and heat will then be transferred from this warmer layer to the outer layers of air. The cooling process in this case would be rather slow since the egg would always be blanketed by warm air, and it would have no direct contact with the cooler air farther away. We may not notice any air motion in the vicinity of the egg, but careful measurements indicate otherwise.
The temperature of the air adjacent to the egg is higher, and thus its density is lower, since at constant pressure the density of a gas is inversely proportional to its temperature. Thus, we have a situation in which some low-density or “light” gas is surrounded by a high-density or “heavy” gas, and the natural laws dictate that the light gas rise. This is no different than the oil in a vine- gar-and-oil salad dressing rising to the top (since roil < rvinegar). This phe- nomenon is characterized incorrectly by the phrase “heat rises,” which is understood to mean heated air rises. The space vacated by the warmer air in
the vicinity of the egg is replaced by the cooler air nearby, and the presence of cooler air in the vicinity of the egg speeds up the cooling process. The rise of warmer air and the flow of cooler air into its place continues until the egg is cooled to the temperature of the surrounding air. The motion that results from the continual replacement of the heated air in the vicinity of the egg by the cooler air nearby is called a natural convection current, and the heat transfer that is enhanced as a result of this natural convection current is called natural convection heat transfer. Note that in the absence of natural convection currents, heat transfer from the egg to the air surrounding it would be by conduction only, and the rate of heat transfer from the egg would be much lower.
Natural convection is just as effective in the heating of cold surfaces in a warmer environment as it is in the cooling of hot surfaces in a cooler environment, as shown in Fig. 20–2. Note that the direction of fluid motion is reversed in this case.
In a gravitational field, there is a net force that pushes upward a light fluid placed in a heavier fluid. The upward force exerted by a fluid on a body
completely or partially immersed in it is called the buoyancy force. The magnitude of the buoyancy force is equal to the weight of the fluid displaced by the body. That is,![]()
where rfluid is the average density of the fluid (not the body), g is the gravitational acceleration, and Vbody is the volume of the portion of the body immersed in the fluid (for bodies completely immersed in the fluid, it is the total volume of the body). In the absence of other forces, the net vertical force acting on a body is the difference between the weight of the body and the buoyancy force. That is,
Note that this force is proportional to the difference in the densities of the fluid and the body immersed in it. Thus, a body immersed in a fluid will experience a “weight loss” in an amount equal to the weight of the fluid it displaces. This is known as Archimedes’ principle.
To have a better understanding of the buoyancy effect, consider an egg dropped into water. If the average density of the egg is greater than the density of water (a sign of freshness), the egg will settle at the bottom of the container. Otherwise, it will rise to the top. When the density of the egg equals the density of water, the egg will settle somewhere in the water while remaining completely immersed, acting like a “weightless object” in space. This occurs when the upward buoyancy force acting on the egg equals the weight of the egg, which acts downward.
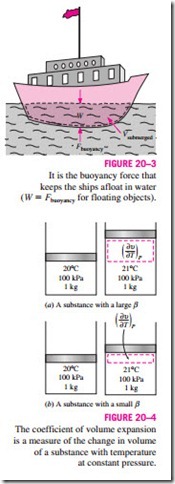
The buoyancy effect has far-reaching implications in life. For one thing, without buoyancy, heat transfer between a hot (or cold) surface and the fluid surrounding it would be by conduction instead of by natural convection. The natural convection currents encountered in the oceans, lakes, and the atmos- phere owe their existence to buoyancy. Also, light boats as well as heavy war- ships made of steel float on water because of buoyancy (Fig. 20–3). Ships are designed on the basis of the principle that the entire weight of a ship and its contents is equal to the weight of the water that the submerged volume of the ship can contain. The “chimney effect” that induces the upward flow of hot combustion gases through a chimney is also due to the buoyancy effect, and the upward force acting on the gases in the chimney is proportional to the difference between the densities of the hot gases in the chimney and the cooler air outside. Note that there is no gravity in space, and thus there can be no natural convection heat transfer in a spacecraft, even if the spacecraft is filled with atmospheric air.
In heat transfer studies, the primary variable is temperature, and it is desirable to express the net buoyancy force (Eq. 20–2) in terms of temperature differences. But this requires expressing the density difference in terms of a temperature difference, which requires a knowledge of a property that represents the variation of the density of a fluid with temperature at constant pressure. The property that provides that information is the volume expansion coefficient b, defined as (Fig. 20–4)
In natural convection studies, the condition of the fluid sufficiently far from the hot or cold surface is indicated by the subscript “infinity” to serve as a re- minder that this is the value at a distance where the presence of the surface is not felt. In such cases, the volume expansion coefficient can be expressed approximately by replacing differential quantities by differences as
where T is the absolute temperature. Note that a large value of b for a fluid means a large change in density with temperature, and that the product b !:T represents the fraction of volume change of a fluid that corresponds to a tem- perature change !:T at constant pressure. Also note that the buoyancy force is proportional to the density difference, which is proportional to the temperature difference at constant pressure. Therefore, the larger the temperature differ- ence between the fluid adjacent to a hot (or cold) surface and the fluid away from it, the larger the buoyancy force and the stronger the natural convection currents, and thus the higher the heat transfer rate.
The magnitude of the natural convection heat transfer between a surface and a fluid is directly related to the flow rate of the fluid. The higher the flow rate, the higher the heat transfer rate. In fact, it is the very high flow rates that in- crease the heat transfer coefficient by orders of magnitude when forced convection is used. In natural convection, no blowers are used, and therefore the flow rate cannot be controlled externally. The flow rate in this case is established by the dynamic balance of buoyancy and friction.
As we have discussed earlier, the buoyancy force is caused by the density difference between the heated (or cooled) fluid adjacent to the surface and the fluid surrounding it, and is proportional to this density difference and the volume occupied by the warmer fluid. It is also well known that whenever two bodies in contact (solid–solid, solid–fluid, or fluid–fluid) move relative to each other, a friction force develops at the contact surface in the direction opposite to that of the motion. This opposing force slows down the fluid and thus reduces the flow rate of the fluid. Under steady conditions, the airflow rate driven by buoyancy is established at the point where these two effects balance each other. The friction force increases as more and more solid surfaces are introduced, seriously disrupting the fluid flow and heat transfer. For that reason, heat sinks with closely spaced fins are not suitable for natural convection cooling.
Most heat transfer correlations in natural convection are based on experimental measurements. The instrument often used in natural convection experiments is the Mach–Zehnder interferometer, which gives a plot of isotherms in the fluid in the vicinity of a surface. The operation principle of interferometers is based on the fact that at low pressure, the lines of constant temperature for a gas correspond to the lines of constant density, and that the index of refraction of a gas is a function of its density. Therefore, the degree of refraction of light at some point in a gas is a measure of the temperature gradient at that point. An interferometer produces a map of interference fringes, which can be interpreted as lines of constant temperature as shown in Fig. 20–5. The smooth and parallel lines in (a) indicate that the flow is laminar, whereas the eddies and irregularities in (b) indicate that the flow is turbulent. Note that the lines are closest near the surface, indicating a higher temperature gradient.
Incoming search terms:
- physical mechanism of natural convection
- mechanism of free convection
- mechanism of natural convection
- physical mechanism of natural (free)convection
- Physical mechanism for free convection
- 3) mechanism of natural convection
- what is mechanism of natural convection?
- physical mechanism of natural convection from forced convection
- physical mechanism of natural convection books
- natural convection mechanism
- mechanism of natural convection heat transfer
- mechanism of force and natural convection
- in natural convection a heated portion of fluid moves because
- heat transfer in natural convection description about that machine
- different mechanisms of natural convection
- what is the mechanism of natural convection heat transfer