AIR DRYERS
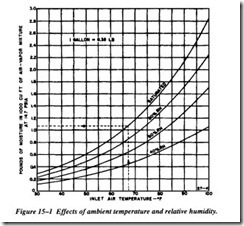
Air entering the first stage of any air compressor carries with it a certain amount of native moisture. This is unavoidable, although the quantity carried will vary widely with the ambient temperature and relative humidity. Figure 15-1 shows the effect of ambient temperature and relative humidity on the quantity of moisture in atmospheric air entering a compressor at 14.7 psia. Under any given conditions, the amount of water vapor entering the compressor per 1,000 cubic feet of mixture may be approxi mated from these curves.
In any air-vapor mixture, each component has its own partial pressure and the air and the vapor are each indifferent to the existence of the other. It follows that the conditions of either component may be studied without reference to the other. In a certain volume of mixture, each component fills the full volume at its own partial pressure. The water vapor may saturate this space, or it may be superheated.
As this vapor is compressed, its volume is reduced; at the same time the temperature automatically increases. As a result, the vapor becomes superheated. More pounds of vapor are now contained in one cubic foot than when the vapor originally entered the compressor.
Under the laws of vapor, the maximum quantity of a particular vapor a given space can contain is dependent solely upon the vapor temperature. As the compressed water vapor is cooled, it will eventually reach the temperature at which the space becomes saturated, now containing the maximum it can hold. Any further cooling will force part of the vapor to condense into its liquid form-water.
The curves contained in Figure 15-2 show what happens over a wide range of pres sures and temperatures. However, these are saturated vapor curves based on starting with 1,000 cubic feet of saturated air. If the air is not saturated at the compressor’s inlet, and it usually is not, use Figure 15-3 to obtain the initial water vapor weight
entering the system per 1,000 cubic feet of compressed air. By reading left on Figure 15-4 from the juncture of the final pressure and final temperature, obtain the maxi mum weight of vapor that this same 1,000 cubic feet can hold after compression and cooling to saturation. If the latter is less than the former, the difference will be condensed. If the latter is higher, there will be no condensation. It is clearly evident that the lower the temperature and the greater the pressure of compressed air, the greater will be the amount of vapor condensed.