PHASE-CHANGE PROCESSES OF PURE SUBSTANCES
There are many practical situations where two phases of a pure substance co- exist in equilibrium. Water exists as a mixture of liquid and vapor in the boiler and the condenser of a steam power plant. The refrigerant turns from liquid to vapor in the freezer of a refrigerator. Even though many home owners con- sider the freezing of water in underground pipes as the most important phase- change process, attention in this section is focused on the liquid and vapor phases and the mixture of these two. As a familiar substance, water will be used to demonstrate the basic principles involved. Remember, however, that all pure substances exhibit the same general behavior.
Compressed Liquid and Saturated Liquid
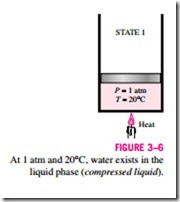
Consider a piston-cylinder device containing liquid water at 20°C and 1 atm pressure (state 1, Fig. 3–6). Under these conditions, water exists in the liquid phase, and it is called a compressed liquid, or a subcooled liquid, meaning
that it is not about to vaporize. Heat is now transferred to the water until its temperature rises to, say, 40°C. As the temperature rises, the liquid water expands slightly, and so its specific volume increases. To accommodate this ex- pansion, the piston will move up slightly. The pressure in the cylinder remains constant at 1 atm during this process since it depends on the outside barometric pressure and the weight of the piston, both of which are constant. Water is still a compressed liquid at this state since it has not started to vaporize.
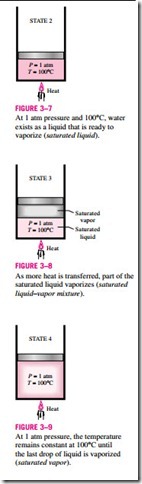
As more heat is transferred, the temperature will keep rising until it reaches 100°C (state 2, Fig. 3–7). At this point water is still a liquid, but any heat addition will cause some of the liquid to vaporize. That is, a phase-change process from liquid to vapor is about to take place. A liquid that is about to vaporize is called a saturated liquid. Therefore, state 2 is a saturated liquid state.
Saturated Vapor and Superheated Vapor
Once boiling starts, the temperature will stop rising until the liquid is completely vaporized. That is, the temperature will remain constant during the en- tire phase-change process if the pressure is held constant. This can easily be verified by placing a thermometer into boiling water on top of a stove. At sea level (P = 1 atm), the thermometer will always read 100°C if the pan is un- covered or covered with a light lid. During a boiling process, the only change we will observe is a large increase in the volume and a steady decline in the liquid level as a result of more liquid turning to vapor.
Midway about the vaporization line (state 3, Fig. 3–8), the cylinder contains equal amounts of liquid and vapor. As we continue transferring heat, the va- porization process will continue until the last drop of liquid is vaporized (state 4, Fig. 3–9). At this point, the entire cylinder is filled with vapor that is on the borderline of the liquid phase. Any heat loss from this vapor will cause some of the vapor to condense (phase change from vapor to liquid). A vapor that is about to condense is called a saturated vapor. Therefore, state 4 is a saturated vapor state. A substance at states between 2 and 4 is often referred to as a saturated liquid–vapor mixture since the liquid and vapor phases coexist in equilibrium at these states.
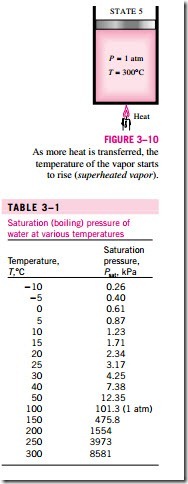
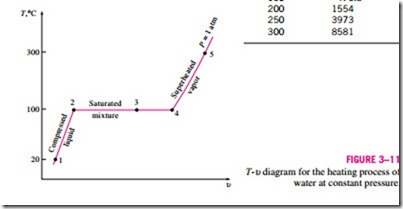
Once the phase-change process is completed, we are back to a single-phase region again (this time vapor), and further transfer of heat will result in an in- crease in both the temperature and the specific volume (Fig. 3–10). At state 5, the temperature of the vapor is, let us say, 300°C; and if we transfer some heat from the vapor, the temperature may drop somewhat but no condensation will take place as long as the temperature remains above 100°C (for P = 1 atm). A vapor that is not about to condense (i.e., not a saturated vapor) is called a superheated vapor. Therefore, water at state 5 is a superheated vapor. This constant-pressure phase-change process as described is illustrated on a T–u diagram in Fig. 3–11.
If the entire process described here is reversed by cooling the water while maintaining the pressure at the same value, the water will go back to state 1, retracing the same path, and in so doing, the amount of heat released will exactly match the amount of heat added during the heating process.
In our daily life, water implies liquid water and steam implies water vapor. In thermodynamics, however, both water and steam usually mean only one thing: H2O.
Saturation Temperature and Saturation Pressure
It probably came as no surprise to you that water started to boil at 100°C.
Strictly speaking, the statement “water boils at 100°C’’ is incorrect. The correct statement is “water boils at 100°C at 1 atm pressure.’’ The only reason the water started boiling at 100°C was because we held the pressure constant at 1 atm (101.325 kPa). If the pressure inside the cylinder were raised to 500 kPa by adding weights on top of the piston, the water would start boiling at 151.9°C. That is, the temperature at which water starts boiling depends on the pressure; therefore, if the pressure is fixed, so is the boiling temperature.
At a given pressure, the temperature at which a pure substance changes phase is called the saturation temperature Tsat. Likewise, at a given temper-
ature, the pressure at which a pure substance changes phase is called the saturation pressure Psat. At a pressure of 101.325 kPa, Tsat is 100°C. Conversely, at a temperature of 100°C, Psat is 101.325 kPa.
Saturation tables that list the saturation pressure against the temperature (or the saturation temperature against the pressure) are available for practically all substances. A partial listing of such a table is given in Table 3–1 for water. This table indicates that the pressure of water changing phase (boiling or condensing) at 25°C must be 3.17 kPa, and the pressure of water must be maintained at 3973 kPa (about 40 atm) to have it boil at 250°C. Also, water can be frozen by dropping its pressure below 0.61 kPa.
It takes a large amount of energy to melt a solid or vaporize a liquid. The amount of energy absorbed or released during a phase-change process is called the latent heat. More specifically, the amount of energy absorbed dur- ing melting is called the latent heat of fusion and is equivalent to the amount of energy released during freezing. Similarly, the amount of energy absorbed during vaporization is called the latent heat of vaporization and is equivalent to the energy released during condensation. The magnitudes of the latent heats depend on the temperature or pressure at which the phase change occurs. At 1 atm pressure, the latent heat of fusion of water is 333.7 kJ/kg and the latent heat of vaporization is 2257.1 kJ/kg.
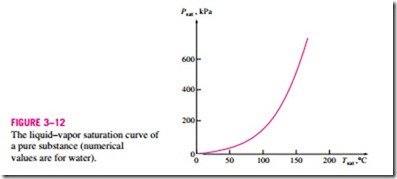
During a phase-change process, pressure and temperature are obviously dependent properties, and there is a definite relation between them, that is,
Tsat = f(Psat). A plot of Tsat versus Psat, such as the one given for water in Fig. 3–12, is called a liquid–vapor saturation curve. A curve of this kind is characteristic of all pure substances.
It is clear from Fig. 3–12 that Tsat increases with Psat. Thus, a substance at higher pressures will boil at higher temperatures. In the kitchen, higher boil- ing temperatures mean shorter cooking times and energy savings. A beef stew, for example, may take 1 to 2 h to cook in a regular pan that operates at 1 atm pressure, but only 20 min in a pressure cooker operating at 3 atm absolute pressure (corresponding boiling temperature: 134°C).
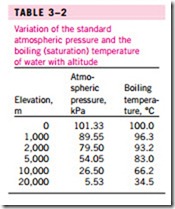
The atmospheric pressure, and thus the boiling temperature of water, de- creases with elevation. Therefore, it takes longer to cook at higher altitudes than it does at sea level (unless a pressure cooker is used). For example, the standard atmospheric pressure at an elevation of 2000 m is 79.50 kPa, which corresponds to a boiling temperature of 93.2°C as opposed to 100°C at sea level (zero elevation). The variation of the boiling temperature of water with altitude at standard atmospheric conditions is given in Table 3–2. For each 1000 m increase in elevation, the boiling temperature drops by a little over 3°C. Note that the atmospheric pressure at a location, and thus the boiling temperature, changes slightly with the weather conditions. But the corresponding change in the boiling temperature is no more than about 1°C.
Some Consequences of Tsat and Psat Dependence
We mentioned earlier that a substance at a specified pressure will boil at the saturation temperature corresponding to that pressure. This phenomenon al- lows us to control the boiling temperature of a substance by simply control- ling the pressure, and it has numerous applications in practice. Below we give some examples. In most cases, the natural drive to achieve phase equilibrium by allowing some liquid to evaporate is at work behind the scenes.
Consider a sealed can of liquid refrigerant-134a in a room at 25°C. If the can has been in the room long enough, the temperature of the refrigerant in the can will also be 25°C. Now, if the lid is opened slowly and some refrigerant is allowed to escape, the pressure in the can will start dropping until it reaches the atmospheric pressure. If you are holding the can, you will notice its temperature dropping rapidly, and even ice forming outside the can if the air is hu- mid. A thermometer inserted in the can will register -26°C when the pressure drops to 1 atm, which is the saturation temperature of refrigerant-134a at that pressure. The temperature of the liquid refrigerant will remain at -26°C until the last drop of it vaporizes.
Another aspect of this interesting physical phenomenon is that a liquid can- not vaporize unless it absorbs energy in the amount of the latent heat of va- porization, which is 217 kJ/kg for refrigerant-134a at 1 atm. Therefore, the rate of vaporization of the refrigerant depends on the rate of heat transfer to the can: the larger the rate of heat transfer, the higher the rate of vaporization. The rate of heat transfer to the can and thus the rate of vaporization of the re- frigerant can be minimized by insulating the can heavily. In the limiting case of no heat transfer, the refrigerant will remain in the can as a liquid at -26°C indefinitely.
The boiling temperature of nitrogen at atmospheric pressure is -196°C (see Table A–3a). This means the temperature of liquid nitrogen exposed to the at- mosphere must be -196°C since some nitrogen will be evaporating. The tem- perature of liquid nitrogen will remain constant at -196°C until it is depleted. For this reason, nitrogen is commonly used in low-temperature scientific stud- ies (such as superconductivity) and cryogenic applications to maintain a test chamber at a constant temperature of -196°C. This is done by placing the test chamber into a liquid nitrogen bath that is open to the atmosphere. Any heat transfer from the environment to the test section is absorbed by the nitrogen, which evaporates isothermally and keeps the test chamber temperature con- stant at -196°C (Fig. 3–13). The entire test section must be insulated heavily to minimize heat transfer and thus liquid nitrogen consumption. Liquid nitro- gen is also used for medical purposes to burn off unsightly spots on the skin. This is done by soaking a cotton swap in liquid nitrogen and wetting the target area with it. As the nitrogen evaporates, it freezes the affected skin by rapidly absorbing heat from it.
based on reducing the pressure of the sealed cooling chamber to the saturation pressure at the desired low temperature and evaporating some water from the products to be cooled. The heat of vaporization during evaporation is absorbed from the products, which lowers the product temperature. The satu- ration pressure of water at 0°C is 0.61 kPa, and the products can be cooled to 0°C by lowering the pressure to this level. The cooling rate can be increased by lowering the pressure below 0.61 kPa, but this is not desirable because of the danger of freezing and the added cost.
In vacuum cooling, there are two distinct stages. In the first stage, the prod- ucts at ambient temperature, say at 25°C, are loaded into the chamber, and the operation begins. The temperature in the chamber remains constant until the saturation pressure is reached, which is 3.17 kPa at 25°C. In the second stage that follows, saturation conditions are maintained inside at progressively lower pressures and the corresponding lower temperatures until the desired
ated cooling, and its use is limited to applications that result in much faster cooling. Products with large surface area per unit mass and a high tendency to release moisture such as lettuce and spinach are well-suited for vacuum cool- ing. Products with low surface area to mass ratio are not suitable, especially those that have relatively impervious peels such as tomatoes and cucumbers.
Some products such as mushrooms and green peas can be vacuum cooled successfully by wetting them first.
The vacuum cooling just described becomes vacuum freezing if the vapor pressure in the vacuum chamber is dropped below 0.6 kPa, the saturation
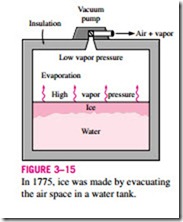
Low vapor pressure Evaporation
pressure of water at 0°C. The idea of making ice by using a vacuum pump is nothing new. Dr. William Cullen actually made ice in Scotland in 1775 by evacuating the air in a water tank (Fig. 3–15).
Package icing is commonly used in small-scale cooling applications to remove heat and keep the products cool during transit by taking advantage of the large latent heat of fusion of water, but its use is limited to products that are not harmed by contact with ice. Also, ice provides moisture as well as refrigeration.
Incoming search terms:
- during the phase change of pure substance
- device working mechanism made by dr william cullen made ice by evacuating air in tank
- explain the phase change process of pure substance
- in 1775 dr william cullenmade ice in Scotland
- phase change processes of pure substances
- procedure of pure substance practical