■ THE THERMODYNAMIC TEMPERATURE SCALE
A temperature scale that is independent of the properties of the substances that are used to measure temperature is called a thermodynamic temperature scale. Such a temperature scale offers great conveniences in thermodynamic calculations, and its derivation is given below using some reversible heat engines.
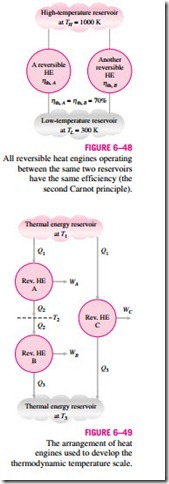
The second Carnot principle discussed in Section 6–9 states that all reversible heat engines have the same thermal efficiency when operating be- tween the same two reservoirs (Fig. 6–48). That is, the efficiency of a reversible engine is independent of the working fluid employed and its properties, the way the cycle is executed, or the type of reversible engine used. Since energy reservoirs are characterized by their temperatures, the thermal efficiency of reversible heat engines is a function of the reservoir temperatures only. That is,
since hth = 1 – QL/QH. In these relations TH and TL are the temperatures of the high- and low-temperature reservoirs, respectively.
The functional form of f (TH, TL) can be developed with the help of the three reversible heat engines shown in Fig. 6–49. Engines A and C are supplied with the same amount of heat Q1 from the high-temperature reservoir at T1. Engine
ηth, A = ηth, B = 70%
Low-temperature reservoir at TL = 300 K Thermal energy reservoir at T1
C rejects Q3 to the low-temperature reservoir at T3. Engine B receives the heat Q2 rejected by engine A at temperature T2 and rejects heat in the amount of Q3 to a reservoir at T3.
The amounts of heat rejected by engines B and C must be the same since engines A and B can be combined into one reversible engine operating be- tween the same reservoirs as engine C and thus the combined engine will have the same efficiency as engine C. Since the heat input to engine C is the same as the heat input to the combined engines A and B, both systems must reject the same amount of heat.
Applying Eq. 6–15 to all three engines separately, we obtain
A careful examination of this equation reveals that the left-hand side is a function of T1 and T3, and therefore the right-hand side must also be a function of T1 and T3 only, and not T2. That is, the value of the product on the right-hand side of this equation is independent of the value of T2. This condition will be satisfied only if the function f has the following form:
engines used to develop the thermodynamic temperature scale.
so that f(T2) will cancel from the product of f (T1, T2) and f (T2, T3), yielding
This temperature scale is called the Kelvin scale, and the temperatures on this scale are called absolute temperatures. On the Kelvin scale, the temperature ratios depend on the ratios of heat transfer between a reversible heat engine and the reservoirs and are independent of the physical properties of any sub- stance. On this scale, temperatures vary between zero and infinity.
The thermodynamic temperature scale is not completely defined by Eq. 6–18 since it gives us only a ratio of absolute temperatures. We also need to know the magnitude of a kelvin. At the International Conference on Weights and Measures held in 1954, the triple point of water (the state at which all three phases of water exist in equilibrium) was assigned the value 273.16 K (Fig. 6–51). The magnitude of a kelvin is defined as 1/273.16 of the tempera- ture interval between absolute zero and the triple-point temperature of water. The magnitudes of temperature units on the Kelvin and Celsius scales are identical (1 K – 1°C). The temperatures on these two scales differ by a con- stant 273.15:
Even though the thermodynamic temperature scale is defined with the help of the reversible heat engines, it is not possible, nor is it practical, to actually operate such an engine to determine numerical values on the absolute temperature scale. Absolute temperatures can be measured accurately by other means, such as the constant-volume ideal-gas thermometer together with extrapolation techniques. The validity of Eq. 6–18 can be demonstrated from physical considerations for a reversible cycle using an ideal gas as the working fluid.