ENTROPY:MINIMIZING THE COMPRESSOR WORK

■ MINIMIZING THE COMPRESSOR WORK

We have just shown that the work input to a compressor is minimized when the compression process is executed in an internally reversible manner. When the changes in kinetic and potential energies are negligible, the compressor work is given by (Eq. 7–53)

Obviously one way of minimizing the compressor work is to approach an internally reversible process as much as possible by minimizing the irreversibilities such as friction, turbulence, and nonquasi-equilibrium compression. The extent to which this can be accomplished is limited by economic considerations. A second (and more practical) way of reducing the compressor work is to keep the specific volume of the gas as small as possible during the compression process. This is done by maintaining the temperature of the gas as low as possible during compression since the specific volume of a gas is proportional to temperature. Therefore, reducing the work input to a compressor requires that the gas be cooled as it is compressed.

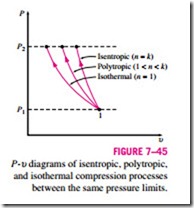
To have a better understanding of the effect of cooling during the compression process, we compare the work input requirements for three kinds of processes: an isentropic process (involves no cooling), a polytropic process (involves some cooling), and an isothermal process (involves maximum cool- ing). Assuming all three processes are executed between the same pressure levels (P1 and P2) in an internally reversible manner and the gas behaves as an ideal gas (Pu = RT) with constant specific heats, we see that the compression work is determined by performing the integration in Eq. 7–56 for each case, with the following results:

The three processes are plotted on a P–u diagram in Fig. 7–45 for the same inlet state and exit pressure. On a P-u diagram, the area to the left of the process curve is the integral of u dP. Thus it is a measure of the steady-flow compression work. It is interesting to observe from this diagram that of P2 the three internally reversible cases considered, the adiabatic compression

(Pu k = constant) requires the maximum work and the isothermal compression (T = constant or Pu = constant) requires the minimum. The work input requirement for the polytropic case (Pu n = constant) is between these two and decreases as the polytropic exponent n is decreased, by increasing the heat rejection during the compression process. If sufficient heat is removed, the value of n approaches unity and the process becomes isothermal. One common way of cooling the gas during compression is to use cooling jackets around the casing of the compressors.

Multistage Compression with Intercooling

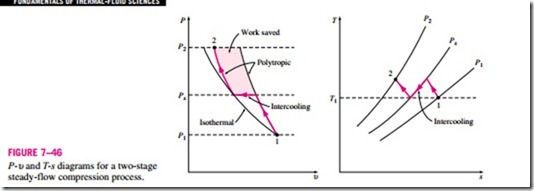
It is clear from these arguments that cooling a gas as it is compressed is desirable since this reduces the required work input to the compressor. However, often it is not possible to have adequate cooling through the casing of the compressor, and it becomes necessary to use other techniques to achieve effective cooling. One such technique is multistage compression with inter- cooling, where the gas is compressed in stages and cooled between each stage by passing it through a heat exchanger called an intercooler. Ideally, the cooling process takes place at constant pressure, and the gas is cooled to the initial temperature T1 at each intercooler. Multistage compression with intercooling is especially attractive when a gas is to be compressed to very high pressures. The effect of intercooling on compressor work is graphically illustrated on P-u and T-s diagrams in Fig. 7–46 for a two-stage compressor. The gas is compressed in the first stage from P1 to an intermediate pressure Px, cooled at constant pressure to the initial temperature T1, and compressed in the second stage to the final pressure P2. The compression processes, in general, can be modeled as polytropic (Pu n = constant) where the value of n varies be- tween k and 1. The colored area on the P-u diagram represents the work saved as a result of two-stage compression with intercooling. The process paths for single-stage isothermal and polytropic processes are also shown for comparison.

The size of the colored area (the saved work input) varies with the value of the intermediate pressure Px, and it is of practical interest to determine the conditions under which this area is maximized. The total work input for a two- stage compressor is the sum of the work inputs for each stage of compression, as determined from Eq. 7–57b:

That is, to minimize compression work during two-stage compression, the pressure ratio across each stage of the compressor must be the same. When this condition is satisfied, the compression work at each stage becomes identical, that is, wcomp I, in = wcomp II, in.