THE CARNOT PRINCIPLES
The second law of thermodynamics puts limits on the operation of cyclic de- vices as expressed by the Kelvin–Planck and Clausius statements. A heat engine cannot operate by exchanging heat with a single reservoir, and a refrigerator cannot operate without a net work input from an external source. We can draw valuable conclusions from these statements. Two conclusions pertain to the thermal efficiency of reversible and irreversible (i.e., actual) heat engines, and they are known as the Carnot principles (Fig. 6–46), expressed as follows:
1. The efficiency of an irreversible heat engine is always less than the efficiency of a reversible one operating between the same two reservoirs.
2. The efficiencies of all reversible heat engines operating between the same two reservoirs are the same.
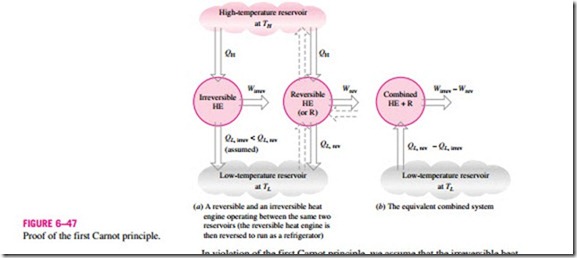
These two statements can be proved by demonstrating that the violation of either statement results in the violation of the second law of thermodynamics. To prove the first statement, consider two heat engines operating between the same reservoirs, as shown in Fig. 6–47. One engine is reversible and the other is irreversible. Now each engine is supplied with the same amount of heat QH. The amount of work produced by the reversible heat engine is Wrev, and the amount produced by the irreversible one is Wirrev.
In violation of the first Carnot principle, we assume that the irreversible heat engine is more efficient than the reversible one (that is, hth, irrev > hth, rev) and thus delivers more work than the reversible one. Now let the reversible heat engine be reversed and operate as a refrigerator. This refrigerator will receive a work input of Wrev and reject heat to the high-temperature reservoir. Since the refrigerator is rejecting heat in the amount of QH to the high-temperature reservoir and the irreversible heat engine is receiving the same amount of heat from this reservoir, the net heat exchange for this reservoir is zero. Thus, it could be eliminated by having the refrigerator discharge QH directly into the irreversible heat engine.
Now considering the refrigerator and the irreversible engine together, we have an engine that produces a net work in the amount of Wirrev – Wrev while exchanging heat with a single reservoir—a violation of the Kelvin–Planck statement of the second law. Therefore, our initial assumption that hth, irrev > hth, rev is incorrect. Then we conclude that no heat engine can be more efficient than a reversible heat engine operating between the same reservoirs.
The second Carnot principle can also be proved in a similar manner. This time, let us replace the irreversible engine by another reversible engine that is more efficient and thus delivers more work than the first reversible engine. By following through the same reasoning, we will end up having an engine that produces a net amount of work while exchanging heat with a single reservoir, which is a violation of the second law. Therefore, we conclude that no reversible heat engine can be more efficient than a reversible one operating be- tween the same two reservoirs, regardless of how the cycle is completed or the kind of working fluid used.