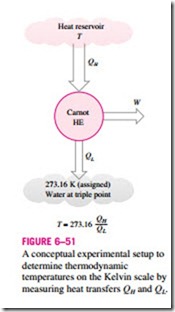
THE CARNOT HEAT ENGINE
The hypothetical heat engine that operates on the reversible Carnot cycle is called the Carnot heat engine. The thermal efficiency of any heat engine, reversible or irreversible, is given by Eq. 6–6 as
where QH is heat transferred to the heat engine from a high-temperature reservoir at TH, and QL is heat rejected to a low-temperature reservoir at TL. For reversible heat engines, the heat transfer ratio in the above relation can be replaced by the ratio of the absolute temperatures of the two reservoirs, as given by Eq. 6–18. Then the efficiency of a Carnot engine, or any reversible heat engine, becomes
This relation is often referred to as the Carnot efficiency, since the Carnot heat engine is the best known reversible engine. This is the highest efficiency a heat engine operating between the two thermal energy reservoirs at temperatures TL and TH can have (Fig. 6–52). All irreversible (i.e., actual) heat engines operating between these temperature limits (TL and TH) will have lower efficiencies. An actual heat engine cannot reach this maximum theoretical efficiency value because it is impossible to completely eliminate all the irreversibilities associated with the actual cycle.
Note that TL and TH in Eq. 6–20 are absolute temperatures. Using °C or °F for temperatures in this relation will give results grossly in error.
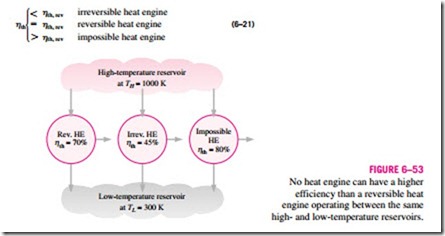
The thermal efficiencies of actual and reversible heat engines operating be- tween the same temperature limits compare as follows (Fig. 6–53):
Most work-producing devices (heat engines) in operation today have efficiencies under 40 percent, which appear low relative to 100 percent. However, when the performance of actual heat engines is assessed, the efficiencies should not be compared to 100 percent; instead, they should be compared to the efficiency of a reversible heat engine operating between the same temperature limits—because this is the true theoretical upper limit for the efficiency, not 100 percent.
The maximum efficiency of a steam power plant operating between TH = 750 K and TL = 300 K is 60 percent, as determined from Eq. 6–20. Compared with this value, an actual efficiency of 40 percent does not seem so bad, even though there is still plenty of room for improvement.
It is obvious from Eq. 6–20 that the efficiency of a Carnot heat engine in- creases as TH is increased, or as TL is decreased. This is to be expected since as TL decreases, so does the amount of heat rejected, and as TL approaches zero, the Carnot efficiency approaches unity. This is also true for actual heat engines. The thermal efficiency of actual heat engines can be maximized by supplying heat to the engine at the highest possible temperature (limited by material strength) and rejecting heat from the engine at the lowest possible temperature (limited by the temperature of the cooling medium such as rivers, lakes, or the atmosphere).
The Quality of Energy
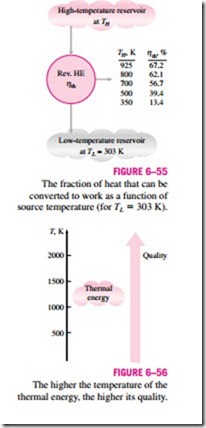
The Carnot heat engine in Example 6–6 receives heat from a source at 925 K and converts 67.2 percent of it to work while rejecting the rest (32.8 percent) to a sink at 303 K. Now let us examine how the thermal efficiency varies with the source temperature when the sink temperature is held constant.
The thermal efficiency of a Carnot heat engine that rejects heat to a sink at 303 K is evaluated at various source temperatures using Eq. 6–20 and is listed in Fig. 6–55. Clearly the thermal efficiency decreases as the source tempera- ture is lowered. When heat is supplied to the heat engine at 500 instead of 925 K, for example, the thermal efficiency drops from 67.2 to 39.4 percent. That is, the fraction of heat that can be converted to work drops to 39.4 per- cent when the temperature of the source drops to 500 K. When the source temperature is 350 K, this fraction becomes a mere 13.4 percent.
These efficiency values show that energy has quality as well as quantity. It is clear from the thermal efficiency values in Fig. 6–55 that more of the high- temperature thermal energy can be converted to work. Therefore, the higher the temperature, the higher the quality of the energy (Fig. 6–56).
Large quantities of solar energy, for example, can be stored in large bodies of water called solar ponds at about 350 K. This stored energy can then be supplied to a heat engine to produce work (electricity). However, the efficiency of solar pond power plants is very low (under 5 percent) because of the low quality of the energy stored in the source, and the construction and maintenance costs are relatively high. Therefore, they are not competitive even though the energy supply of such plants is free. The temperature (and thus the quality) of the solar energy stored could be raised by utilizing concentrating collectors, but the equipment cost in that case becomes very high.
Work is a more valuable form of energy than heat since 100 percent of work can be converted to heat, but only a fraction of heat can be converted to work. When heat is transferred from a high-temperature body to a lower-temperature one, it is degraded since less of it now can be converted to work. For example, if 100 kJ of heat is transferred from a body at 1000 K to a body at 300 K, at the end we will have 100 kJ of thermal energy stored at 300 K, which has no practical value. But if this conversion is made through a heat engine, up to 1 – 300/1000 = 70 percent of it could be converted to work, which is a more valuable form of energy. Thus 70 kJ of work potential is wasted as a result of this heat transfer, and energy is degraded.
Quantity versus Quality in Daily Life
At times of energy crisis, we are bombarded with speeches and articles on how to “conserve” energy. Yet we all know that the quantity of energy is al- ready conserved. What is not conserved is the quality of energy, or the work potential of energy. Wasting energy is synonymous to converting it to a less useful form. One unit of high-quality energy can be more valuable than three units of lower-quality energy. For example, a finite amount of heat energy at high temperature is more attractive to power plant engineers than a vast amount of heat energy at low temperature, such as the energy stored in the up- per layers of the oceans at tropical climates.
As part of our culture, we seem to be fascinated by quantity, and little attention is given to quality. However, quantity alone cannot give the whole picture, and we need to consider quality as well. That is, we need to look at something from both the first- and second-law points of view when evaluating something, even in nontechnical areas. Below we present some ordinary events and show their relevance to the second law of thermodynamics.
Consider two students Andy and Wendy. Andy has 10 friends who never miss his parties and are always around during fun times. However, they seem to be busy when Andy needs their help. Wendy, on the other hand, has five friends. They are never too busy for her, and she can count on them at times of need. Let us now try to answer the question, Who has more friends? From the first-law point of view, which considers quantity only, it is obvious that Andy has more friends. However, from the second-law point of view, which considers quality as well, there is no doubt that Wendy is the one with more friends.
Another example with which most people will identify is the multibillion- dollar diet industry, which is primarily based on the first law of thermo- dynamics. However, considering that 90 percent of the people who lose weight gain it back quickly, with interest, suggests that the first law alone does not give the whole picture. This is also confirmed by studies that show that calories that come from fat are more likely to be stored as fat than the calories that come from carbohydrates and protein. A Stanford study found that body weight was related to fat calories consumed and not calories per se. A Harvard study found no correlation between calories eaten and degree of obesity. A major Cornell University survey involving 6500 people in nearly all prov- inces of China found that the Chinese eat more—gram for gram, calorie for calorie—than Americans do, but they weigh less, with less body fat. Studies indicate that the metabolism rates and hormone levels change noticeably in the mid 30s. Some researchers concluded that prolonged dieting teaches a body to survive on fewer calories, making it more fuel efficient. This probably explains why the dieters gain more weight than they lost once they go back to their normal eating levels.
People who seem to be eating whatever they want, whenever they want, are living proof that the calorie-counting technique (the first law) leaves many questions on dieting unanswered. Obviously, more research focused on the second-law effects of dieting is needed before we can fully understand the weight-gain and weight-loss process.
It is tempting to judge things on the basis of their quantity instead of their quality since assessing quality is much more difficult than assessing quantity. However, assessments made on the basis of quantity only (the first law) may be grossly inadequate and misleading.