■ THE CARNOT CYCLE
We mentioned earlier that heat engines are cyclic devices and that the working fluid of a heat engine returns to its initial state at the end of each cycle.
Work is done by the working fluid during one part of the cycle and on the working fluid during another part. The difference between these two is the net work delivered by the heat engine. The efficiency of a heat-engine cycle greatly depends on how the individual processes that make up the cycle are executed. The net work, thus the cycle efficiency, can be maximized by using processes that require the least amount of work and deliver the most, that is, by using reversible processes. Therefore, it is no surprise that the most efficient cycles are reversible cycles, that is, cycles that consist entirely of reversible processes.
Reversible cycles cannot be achieved in practice because the irreversibilities associated with each process cannot be eliminated. However, reversible cycles provide upper limits on the performance of real cycles. Heat engines and refrigerators that work on reversible cycles serve as models to which actual heat engines and refrigerators can be compared. Reversible cycles also serve as starting points in the development of actual cycles and are modified as needed to meet certain requirements.
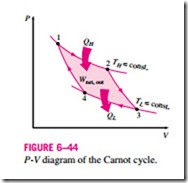
Probably the best known reversible cycle is the Carnot cycle, first proposed in 1824 by French engineer Sadi Carnot. The theoretical heat engine that operates on the Carnot cycle is called the Carnot heat engine. The Carnot cycle is composed of four reversible processes—two isothermal and two adiabatic—and it can be executed either in a closed or a steady-flow system. Consider a closed system that consists of a gas contained in an adiabatic piston-cylinder device, as shown in Fig. 6–43. The insulation of the cylinder head is such that it may be removed to bring the cylinder into contact with reservoirs to provide heat transfer. The four reversible processes that make up the Carnot cycle are as follows:
Reversible Isothermal Expansion (process 1-2, TH = constant).
Initially (state 1), the temperature of the gas is TH and the cylinder head is in close contact with a source at temperature TH. The gas is allowed to expand slowly, doing work on the surroundings. As the gas expands, the temperature of the gas tends to decrease. But as soon as the temperature drops by an infinitesimal amount dT, some heat flows from the reservoir into the gas, raising the gas temperature to TH. Thus, the gas temperature is kept constant at TH. Since the temperature difference between the gas and the reservoir never exceeds a differential amount dT, this is a reversible heat transfer process.
It continues until the piston reaches position 2. The amount of total heat transferred to the gas during this process is QH.
Reversible Adiabatic Expansion (process 2-3, temperature drops from TH to TL). At state 2, the reservoir that was in contact with the cylinder head is removed and replaced by insulation so that the system becomes adiabatic. The gas continues to expand slowly, doing work on the surroundings until its temperature drops from TH to TL (state 3).
The piston is assumed to be frictionless and the process to be quasi- equilibrium, so the process is reversible as well as adiabatic.
Reversible Isothermal Compression (process 3-4, TL = constant).
At state 3, the insulation at the cylinder head is removed, and the cylinder is brought into contact with a sink at temperature TL. Now the piston is pushed inward by an external force, doing work on the gas. As the gas is compressed, its temperature tends to rise. But as soon as it rises by an infinitesimal amount dT, heat flows from the gas to the sink, causing the gas temperature to drop to TL. Thus, the gas temperature is maintained constant at TL. Since the temperature difference between the gas and the sink never exceeds a differential amount dT, this is a reversible heat transfer process. It continues until the piston reaches state 4. The amount of heat rejected from the gas during this process is QL.
Reversible Adiabatic Compression (process 4-1, temperature rises from TL to TH). State 4 is such that when the low-temperature reservoir is removed, the insulation is put back on the cylinder head, and the gas is compressed in a reversible manner, the gas returns to its initial state (state 1). The temperature rises from TL to TH during this reversible adiabatic compression process, which completes the cycle.
The P-V diagram of this cycle is shown in Fig. 6–44. Remembering that on a P-V diagram the area under the process curve represents the boundary work for quasi-equilibrium (internally reversible) processes, we see that the area un-
der curve 1-2-3 is the work done by the gas during the expansion part of the cycle, and the area under curve 3-4-1 is the work done on the gas during the compression part of the cycle. The area enclosed by the path of the cycle (area 1-2-3-4-1) is the difference between these two and represents the net work done during the cycle.
Notice that if we acted stingily and compressed the gas at state 3 adiabatically instead of isothermally in an effort to save QL, we would end up back at state 2, retracing the process path 3-2. By doing so we would save QL, but we would not be able to obtain any net work output from this engine. This illustrates once more the necessity of a heat engine exchanging heat with at least two reservoirs at different temperatures to operate in a cycle and produce a net amount of work.
The Carnot cycle can also be executed in a steady-flow system. It is dis- cussed in later chapters in conjunction with other power cycles.
Being a reversible cycle, the Carnot cycle is the most efficient cycle operating between two specified temperature limits. Even though the Carnot cycle cannot be achieved in reality, the efficiency of actual cycles can be improved by attempting to approximate the Carnot cycle more closely.
The Reversed Carnot Cycle
The Carnot heat-engine cycle just described is a totally reversible cycle.
Therefore, all the processes that comprise it can be reversed, in which case it becomes the Carnot refrigeration cycle. This time, the cycle remains exactly the same, except that the directions of any heat and work interactions are reversed: Heat in the amount of QL is absorbed from the low-temperature reservoir, heat in the amount of QH is rejected to a high-temperature reservoir, and a work input of Wnet, in is required to accomplish all this.
The P-V diagram of the reversed Carnot cycle is the same as the one given for the Carnot cycle, except that the directions of the processes are reversed, as shown in Fig. 6–45.