■ ADIABATIC SATURATION AND WET-BULB TEMPERATURES
Relative humidity and specific humidity are frequently used in engineering and atmospheric sciences, and it is desirable to relate them to easily measurable quantities such as temperature and pressure. One way of determining the
relative humidity is to determine the dew-point temperature of air, as dis- cussed in the last section. Knowing the dew-point temperature, we can deter- mine the vapor pressure Pυ and thus the relative humidity. This approach is simple, but not quite practical.
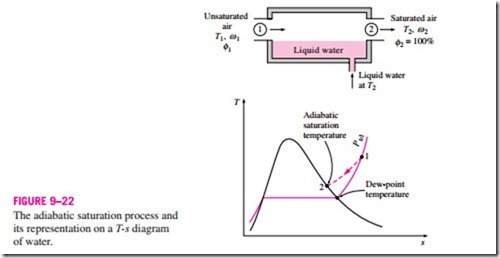
Another way of determining the absolute or relative humidity is related to an adiabatic saturation process, shown schematically and on a T-s diagram in Fig. 9–22. The system consists of a long insulated channel that contains a pool of water. A steady stream of unsaturated air that has a specific humidity of v1 (unknown) and a temperature of T1 is passed through this channel. As the air flows over the water, some water will evaporate and mix with the airstream. The moisture content of air will increase during this process, and its temperature will decrease, since part of the latent heat of vaporization of the water that evaporates will come from the air. If the channel is long enough, the airstream will exit as saturated air (f = 100 percent) at temperature T2, which is called the adiabatic saturation temperature.
If makeup water is supplied to the channel at the rate of evaporation at temperature T2, the adiabatic saturation process described above can be analyzed as a steady-flow process. The process involves no heat or work interactions, and the kinetic and potential energy changes can be neglected. Then the conservation of mass and conservation of energy relations for this two-inlet, one- exit steady-flow system reduces to the following:
since f2 = 100 percent. Thus we conclude that the specific humidity (and relative humidity) of air can be determined from Eqs. 9–35 and 9–36 by measuring the pressure and temperature of air at the inlet and the exit of an adiabatic saturator.
If the air entering the channel is already saturated, then the adiabatic saturation temperature T2 will be identical to the inlet temperature T1, in which case Eq. 9–35 yields v1 = v2. In general, the adiabatic saturation temperature will be between the inlet and dew-point temperatures.
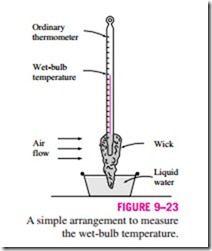
The adiabatic saturation process discussed above provides a means of determining the absolute or relative humidity of air, but it requires a long channel or a spray mechanism to achieve saturation conditions at the exit. A more practical approach is to use a thermometer whose bulb is covered with a cotton wick saturated with water and to blow air over the wick, as shown in Fig. 9–23. The temperature measured in this matter is called the wet-bulb temperature Twb, and it is commonly used in air-conditioning applications. The basic principle involved is similar to that in adiabatic saturation. When unsaturated air passes over the wet wick, some of the water in the wick evaporates. As a result, the temperature of the water drops, creating a temperature difference (which is the driving force for heat transfer) between the air and the water. After a while, the heat loss from the water by evaporation equals the heat gain from the air, and the water temperature stabilizes. The thermometer reading at this point is the wet-bulb temperature. The wet-bulb temperature A simple arrangement to measure the wet-bulb temperature.
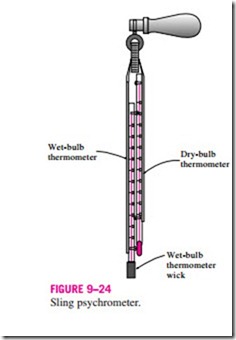
can also be measured by placing the wet-wicked thermometer in a holder attached to a handle and rotating the holder rapidly, that is, by moving the thermometer instead of the air. A device that works on this principle is called a sling psychrometer and is shown in Fig. 9–24. Usually a dry-bulb thermometer is also mounted on the frame of this device so that both the wet- and dry-bulb temperatures can be read simultaneously.
Advances in electronics made it possible to measure humidity directly in a fast and reliable way. It appears that sling psychrometers and wet-wicked thermometers are about to become things of the past. Today, hand-held electronic humidity measurement devices based on the capacitance change in a thin polymer film as it absorbs water vapor are capable of sensing and digitally dis- playing the relative humidity within 1 percent accuracy in a matter of seconds. In general, the adiabatic saturation temperature and the wet-bulb temperature are not the same. However, for air–water-vapor mixtures at atmospheric pressure, the wet-bulb temperature happens to be approximately equal to the adiabatic saturation temperature. Therefore, the wet-bulb temperature Twb can be used in Eq. 9–14 in place of T2 to determine the specific humidity of air.
Incoming search terms:
- adiabatic saturation temp and wet bulb temp are nearly equal
- Wet-Bulb thermometer
- adiabatic saturation enthalpy of moist air
- describe wet bulb temperature with T-S diagram
- how adiabatic saturator used in relative humidity
- wet bulb temp