THE SECOND LA W OF THERMODYNAMICS:REVERSIBLE AND IRREVERSIBLE PROCESSES

REVERSIBLE AND IRREVERSIBLE PROCESSES

The second law of thermodynamics states that no heat engine can have an efficiency of 100 percent. Then one may ask, What is the highest efficiency that a heat engine can possibly have? Before we can answer this question, we need to define an idealized process first, which is called the reversible process.

The processes that were discussed at the beginning of this chapter occurred in a certain direction. Once having taken place, these processes cannot reverse themselves spontaneously and restore the system to its initial state. For this reason, they are classified as irreversible processes. Once a cup of hot coffee

cools, it will not heat up by retrieving the heat it lost from the surroundings. If it could, the surroundings, as well as the system (coffee), would be restored to their original condition, and this would be a reversible process.

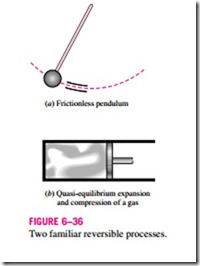
A reversible process is defined as a process that can be reversed without leaving any trace on the surroundings (Fig. 6–36). That is, both the system and the surroundings are returned to their initial states at the end of the reverse process. This is possible only if the net heat and net work exchange between the system and the surroundings is zero for the combined (original and re- verse) process. Processes that are not reversible are called irreversible processes.

It should be pointed out that a system can be restored to its initial state following a process, regardless of whether the process is reversible or irreversible. But for reversible processes, this restoration is made without leaving any net change on the surroundings, whereas for irreversible processes, the surroundings usually do some work on the system and therefore will not return to their original state.

Reversible processes actually do not occur in nature. They are merely idealizations of actual processes. Reversible processes can be approximated by actual devices, but they can never be achieved. That is, all the processes occurring in nature are irreversible. You may be wondering, then, why we are bothering with such fictitious processes. There are two reasons. First, they are easy to analyze, since a system passes through a series of equilibrium states during a reversible process; second, they serve as idealized models to which actual processes can be compared.

In daily life, the concepts of Mr. Right and Ms. Right are also idealizations, just like the concept of a reversible (perfect) process. People who insist on finding Mr. or Ms. Right to settle down are bound to remain Mr. or Ms. Single for the rest of their lives. The possibility of finding the perfect prospective mate is no higher than the possibility of finding a perfect (reversible) process. Likewise, a person who insists on perfection in friends is bound to have no friends.

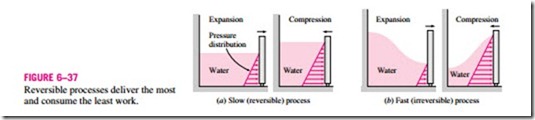
Engineers are interested in reversible processes because work-producing devices such as car engines and gas or steam turbines deliver the most work, and work-consuming devices such as compressors, fans, and pumps consume the least work when reversible processes are used instead of irreversible ones (Fig. 6–37).

Reversible processes can be viewed as theoretical limits for the corresponding irreversible ones. Some processes are more irreversible than others. We may never be able to have a reversible process, but we may certainly approach it. The more closely we approximate a reversible process, the more

work delivered by a work-producing device or the less work required by a work-consuming device.

The concept of reversible processes leads to the definition of the second- law efficiency for actual processes, which is the degree of approximation to the corresponding reversible processes. This enables us to compare the per- formance of different devices that are designed to do the same task on the basis of their efficiencies. The better the design, the lower the irreversibilities and the higher the second-law efficiency.

Irreversibilities

The factors that cause a process to be irreversible are called irreversibilities.

They include friction, unrestrained expansion, mixing of two fluids, heat transfer across a finite temperature difference, electric resistance, inelastic deformation of solids, and chemical reactions. The presence of any of these effects renders a process irreversible. A reversible process involves none of these. Some of the frequently encountered irreversibilities are discussed briefly below.

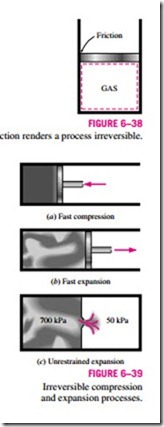
Friction is a familiar form of irreversibility associated with bodies in motion. When two bodies in contact are forced to move relative to each other (a piston in a cylinder, for example, as shown in Fig. 6–38), a friction force that opposes the motion develops at the interface of these two bodies, and some work is needed to overcome this friction force. The energy supplied as work is eventually converted to heat during the process and is transferred to the bodies in contact, as evidenced by a temperature rise at the interface. When the direction of the motion is reversed, the bodies will be restored to their original position, but the interface will not cool, and heat will not be converted back to work. Instead, more of the work will be converted to heat while overcoming the friction forces that also oppose the reverse motion. Since the system (the moving bodies) and the surroundings cannot be returned to their original states, this process is irreversible. Therefore, any process that involves friction is irreversible. The larger the friction forces involved, the more irreversible the process is.

Friction does not always involve two solid bodies in contact. It is also en- countered between a fluid and solid and even between the layers of a fluid moving at different velocities. A considerable fraction of the power produced by a car engine is used to overcome the friction (the drag force) between the air and the external surfaces of the car, and it eventually becomes part of the internal energy of the air. It is not possible to reverse this process and recover that lost power, even though doing so would not violate the conservation of energy principle.

Another example of irreversibility is the unrestrained expansion of a gas separated from a vacuum by a membrane, as shown in Fig. 6–39. When the membrane is ruptured, the gas fills the entire tank. The only way to restore the system to its original state is to compress it to its initial volume, while transferring heat from the gas until it reaches its initial temperature. From the conservation of energy considerations, it can easily be shown that the amount of heat transferred from the gas equals the amount of work done on the gas by the surroundings. The restoration of the surroundings involves conversion of this heat completely to work, which would violate the second law. Therefore, unrestrained expansion of a gas is an irreversible process.

A third form of irreversibility familiar to us all is heat transfer through a finite temperature difference. Consider a can of cold soda left in a warm room (Fig. 6–40). Heat will flow from the warmer room air to the cooler soda. The only way this process can be reversed and the soda restored to its original temperature is to provide refrigeration, which requires some work input. At the end of the reverse process, the soda will be restored to its initial state, but the

(a) n irreversible heat transfer process

surroundings will not be. The internal energy of the surroundings will increase by an amount equal in magnitude to the work supplied to the refrigerator. The restoration of the surroundings to the initial state can be done only by converting this excess internal energy completely to work, which is impossible to do without violating the second law. Since only the system, not both the sys- tem and the surroundings, can be restored to its initial condition, heat transfer through a finite temperature difference is an irreversible process.

Heat transfer can occur only when there is a temperature difference between a system and its surroundings. Therefore, it is physically impossible to have a reversible heat transfer process. But a heat transfer process becomes less and less irreversible as the temperature difference between the two bodies approaches zero. Then heat transfer through a differential temperature difference dT can be considered to be reversible. As dT approaches zero, the process can be reversed in direction (at least theoretically) without requiring any refrigeration. Notice that reversible heat transfer is a conceptual process and cannot be duplicated in the real world.

The smaller the temperature difference between two bodies, the smaller the heat transfer rate will be. Any significant heat transfer through a small temperature difference will require a very large surface area and a very long time. Therefore, even though approaching reversible heat transfer is desirable from a thermodynamic point of view, it is impractical and not economically feasible.

Internally and Externally Reversible Processes

A typical process involves interactions between a system and its surroundings,

and a reversible process involves no irreversibilities associated with either of them.

A process is called internally reversible if no irreversibilities occur within the boundaries of the system during the process. During an internally reversible process, a system proceeds through a series of equilibrium states, and when the process is reversed, the system passes through exactly the same equi- librium states while returning to its initial state. That is, the paths of the for- ward and reverse processes coincide for an internally reversible process. The quasi-equilibrium process is an example of an internally reversible process. A process is called externally reversible if no irreversibilities occur outside the system boundaries during the process. Heat transfer between a reservoir and a system is an externally reversible process if the outer surface of the system is at the temperature of the reservoir.

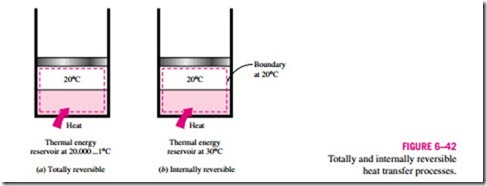
A process is called totally reversible, or simply reversible, if it involves no irreversibilities within the system or its surroundings (Fig. 6–41). A totally reversible process involves no heat transfer through a finite temperature dif- ference, no nonquasi-equilibrium changes, and no friction or other dissipative effects.

As an example, consider the transfer of heat to two identical systems that are undergoing a constant-pressure (thus constant-temperature) phase-change

process, as shown in Fig. 6–42. Both processes are internally reversible, since both take place isothermally and both pass through exactly the same equilibrium states. The first process shown is externally reversible also, since heat transfer for this process takes place through an infinitesimal temperature difference dT. The second process, however, is externally irreversible, since it involves heat transfer through a finite temperature difference dT.