COMPRESSIBILITY FACTOR—A MEASURE OF DEVIATION FROM IDEAL-GAS BEHAVIOR
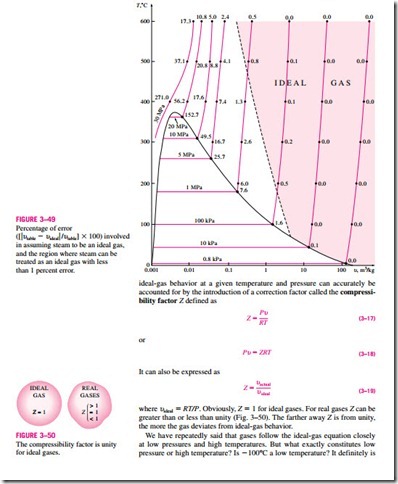
The ideal-gas equation is very simple and thus very convenient to use. But, as illustrated in Fig. 3–49, gases deviate from ideal-gas behavior significantly at states near the saturation region and the critical point. This deviation from
for most substances, but not for air. Air (or nitrogen) can be treated as an ideal gas at this temperature and atmospheric pressure with an error under 1 per- cent. This is because nitrogen is well over its critical temperature (-147°C) and away from the saturation region. At this temperature and pressure, how- ever, most substances would exist in the solid phase. Therefore, the pressure or temperature of a substance is high or low relative to its critical temperature or pressure.
Gases behave differently at a given temperature and pressure, but they behave very much the same at temperatures and pressures normalized with re- spect to their critical temperatures and pressures. The normalization is done as
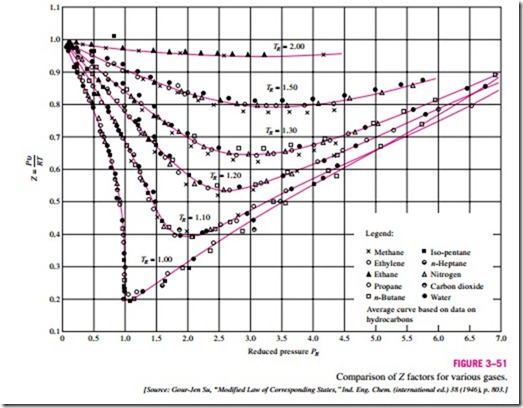
Here PR is called the reduced pressure and TR the reduced temperature. The Z factor for all gases is approximately the same at the same reduced pressure and temperature. This is called the principle of corresponding states. In Fig. 3–51, the experimentally determined Z values are plotted against PR and TR for several gases. The gases seem to obey the principle of corresponding states
reasonably well. By curve-fitting all the data, we obtain the generalized compressibility chart that can be used for all gases (Fig. A–34).
The following observations can be made from the generalized compressibility chart:
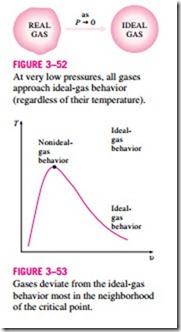
1. At very low pressures (PR 1), the gases behave as an ideal gas regardless of temperature (Fig. 3–52),
2. At high temperatures (TR > 2), ideal-gas behavior can be assumed with good accuracy regardless of pressure (except when PR �1).
3. The deviation of a gas from ideal-gas behavior is greatest in the vicinity of the critical point (Fig. 3–53).
When P and υ, or T and υ, are given instead of P and T, the generalized compressibility chart can still be used to determine the third property, but it would involve tedious trial and error. Therefore, it is necessary to define one more reduced property called the pseudo-reduced specific volume υR as
Note that υR is defined differently from PR and TR. It is related to Tcr and Pcr instead of υcr. Lines of constant υR are also added to the compressibility charts, and this enables one to determine T or P without having to resort to time-consuming iterations (Fig. 3–54).