Density and Specific Gravity
The density of a substance is its weight per unit of volume. The unit of volume in the English system of measurement is 1 cubic foot, or 1 ft3. To find the density of a sub stance, you must know its weight and volume. You then divide its weight by its volume to find the weight per unit volume. In equation form, this is written as
EXAMPLE: The liquid that fills a certain container weighs 1,496.6 pounds. The con tainer is 4 feet long, 3 feet wide, and 2 feet deep. Its volume is 24 cubic feet (4ft x 3 ft x 2 ft). If 24 cubic feet of this liquid weighs 1,497.6 pounds, then 1 cubic foot weighs
or 62.4 pounds. Therefore, the density of the liquid is 62.4 pounds per cubic foot or lb/ft3. This is the density of water at 4T and is usually used as the standard for comparing the densities of other substances. This standard temperature is used when ever the density of liquids and solids is measured. Changes in temperature will not change the weight of a substance but will change the volume of the substance by expansion or contraction, thus changing the weight per unit volume, density.
In physics, the word specific implies a ratio. Weight is the measure of the earth’s attraction for a body, which is called gravity. Thus, the ratio of the weight of a unit volume of some substance to the weight of an equal volume of a standard substance, measured under standard pressure and temperature, is called specific gravity. The terms specific weight and specific density are also sometimes used to express this ratio:
The specific gravity of water is 1.0 or a density of 62.4 lb/ft3 If a cubic foot of a liquid weighs 68.64 pounds, then its specific gravity is 1.1 or
Thus, the specific gravity of the liquid is the ratio of its density to the density of water. If the specific gravity of a liquid or solid is known, the density can be obtained by multiplying its specific gravity by the density of water. For example, if a hydraulic fluid has a specific gravity of 0.8, 1 cubic foot of the fluid weighs 0.8 times the weight of water (62.4 pounds) or 49.92 pounds.
Specific gravity and density are independent of the size of the sample and depend only on the substance of which it is made.
Viscosity
Viscosity is one of the most important properties of hydraulic fluids. It is a measure of a fluid’s resistance to flow. A liquid such as gasoline, which flows easily, has a low viscosity, and a liquid such as tar, which flows slowly, has a high viscosity. The viscosity of a liquid is affected by changes in temperature and pressure. As the tempera ture of liquid increases, its viscosity decreases. That is, a liquid flows more easily when it is hot than when it is cold. The viscosity of a liquid will increase as the pressure on the liquid increases.
A satisfactory liquid for a hydraulic system must be thick enough to give a good seal at pumps, motors, valves, and so on. These components depend on close fits for creating and maintaining pressure. Any internal leakage through these clearances results in loss of pressure, instantaneous control, and pump efficiency. Leakage losses are greater with thinner liquids (low viscosity). A liquid that is too thin will also allow rapid wearing of moving parts, or of parts that operate under heavy loads. On the other hand, if the liquid is too thick, viscosity too high, the internal friction of the liq uid will cause an increase in the liquid’s flow resistance through clearances of closely fitted parts, lines, and internal passages. This results in pressure drops throughout the system, sluggish operation of the equipment, and an increase in power consumption.
Measurement of Viscosity
Viscosity is normally determined by measuring the time required for a fixed volume of a fluid, at a given temperature, to flow through a calibrated orifice or capillary tube. The instruments used to measure the viscosity of a liquid are known as viscosimeters.
In decreasing order of exactness, methods of defining viscosity include absolute (poise) viscosity; kinematic viscosity in centistokes; relative viscosity in Saybolt uni versal seconds (SUS); and SAE numbers.
Absolute Viscosity
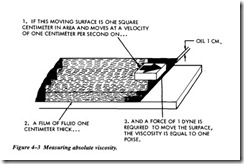
The resistance when moving one layer of liquid over another is the basis for the labo ratory method of measuring absolute viscosity. Poise viscosity is defined as the force (pounds) per unit of area, in square inches, required to move one parallel surface at a speed of one centimeter per second past another parallel surface when the two sur faces are separated by a fluid film 1 centimeter thick (Figure 4-3). In the metric sys tem, force is expressed in dynes and area in square centimeters. Poise is also the ratio between the shearing stress and the rate of shear of the fluid.
Kinematic Viscosity
The concept of kinematic viscosity is the outgrowth of the use of a head of liquid to produce a flow through a capillary tube. The coefficient of absolute viscosity, when divided by the density of the liquid, is called the kinematic viscosity. In the metric system, the unit of viscosity is called the stoke and it has the units of centimeters squared per second. One one-hundredth of a stoke is a centistoke.
relationship between absolute and kinematic viscosity can be stated as:
Incoming search terms:
- hydraulic fluid specific gravity
- density of hydraulic oil
- why is it important to know density of liquids in fluid hydraulics
- hydraulic oil density
- specific volume in hydraulic and fluid mechanics
- sg of hydraulic oil
- specific gravity of water in hydraulics
- specific weight in hydraulics
- what is spcific gravity in pneumatucs and hydroulic
- specific gravity in hydraulic
- specific gravity of different hydraulic oils
- specific gravity of hydraulic fluid
- specific gravity of nectar
- specific gravity of water and hydraulic oil
- Viscosity measuring instruments mail
- specific weight of hydraulic fluid
- what is specific weight in hydraulic fluid?
- what is called fluid specific gravity
- specific gravity hydrolic
- relative density of hydraulic oil
- density lb ft3 from specific gravity
- density of hyfraulic fluid in lb/in^3
- density specific gravity specific weight jn hydraulics
- hydraulic fluid density
- hydraulic fluid has a specific weight of 55 lb/ft3 What is the specific gravity
- Hydraulic Fluids loc:US
- hydraulic oil density versus temperature
- hydraulics specific gravity
- hydrolic fuil specifi
- hydrolics specific gravity formula
- low specific gravity of hydraulic system
- relation between density specific gravity in hydraulics
- define specific gavity in hydraulics