The influence of temperature
In the above figures the influence of temperature was not included, so that the influence of pressure alone could be illustrated, and so it was assumed that all flows and
expansions were isothermal and at the standard reference temperature. In Equations (9.7) and (9.8) the influence of pressure and temperature on actual volumetric flow rate is presented. If the influence of pressure is neglected, in order to separate the effect of temperature, the equation reduces to:
The influence that air temperature can have on volumetric flow rate is shown graphically in Figure 9.17. This is a plot of volumetric flow rate at the reference temperature of 15°C, against actual volumetric flow rate at a given temperature. It should be noted that in Equation (9.14) and Figure 9.17 all pressures are standard atmospheric so that the influence of temperature can be considered in isolation from that of pressure.
It can be seen from Figure 9.17 that small changes in temperature do not have the significant effect on volumetric flow rate that changes in pressure can have. This is because the influence of temperature is in terms of the ratio of absolute temperatures and the 273 that has to be added to the Celsius temperature has a considerable dampening effect.
Air temperatures higher than 100°C can be experienced, however. Air at a temperature of 100°C will result from the compression of air in a positive displacement blower operating at about 1 bar gauge, but from a screw compressor delivering air at 3 bar gauge it could be more than 200°C. In some cases the material to be conveyed may be at a high temperature and this could have a major influence on the air flow rate, and hence conveying air velocity. This particular situation is considered in some detail below.
It will be seen from Equation (9.11) that if the temperature is reduced, then the velocity will fall. This is because the density of the air increases with decrease in temperature. The volumetric flow rate of air that is specified must be sufficient to maintain the desired conveying line inlet air velocity at the lowest temperature anticipated. Due
account, therefore, must be taken of cold start-up and winter operating conditions, particularly with vacuum conveying systems that draw in atmospheric air. This point is illustrated quite forcefully in Figure 9.18.
Figure 9.18 is drawn for a 150 mm bore pipeline and a conveying line inlet air pressure of 1 bar gauge. It will be seen from this that conveying air velocity can be very sensitive to temperature. The average gradient on this plot is about 0.04 m/s per °C temperature change, and so if the temperature of the conveying air was reduced for some reason it could result in pipeline blockage in a system operating with a pick-up velocity close to the minimum conveying air velocity for the given material.
Conveyed material influences
The above analysis refers to the situation with regard to the air only. For the conveying line, however, the material also has to be taken into account, and although the air may be at 20°C, the material to be conveyed may be at 200°C or more. In order to deter- mine the temperature of the conveyed suspension it is necessary to carry out an energy balance. If a control surface is taken around the material feeding device and the immediate pipelines an energy balance gives:
where m is the mass flow rate (kg/s), Cp, is the specific heat (kJ/kg . K), t is the temperature (ºC) and the subscript p refers to conveyed material or particles, a is air, s is suspension.
If heat exchanges with the surroundings, kinetic energies and other minor energy quantities are neglected.
It is the temperature of the suspension, ts, that is required and so a rearrangement gives:
With so many variables it is difficult to illustrate the relationship graphically. One case has been selected, however, for a conveyed material at a temperature of 15°C, and having a specific heat of 1.0 kJ/kg . K. This shows the influence of conveying line inlet air temperature and solids loading ratio on the resulting suspension temperature. It relates to the dilute phase conveying of a material with a positive displacement blower, where the conveying line inlet air temperature might be up to about 100°C. This is shown in Figure 9.19.
Figure 9.19 shows that the solids loading ratio has a dominating effect on the suspension temperature, even with dilute phase conveying. Unless the conveyed material has a very low specific heat value, and is conveyed in very dilute phase, the tempera- ture of the conveyed suspension will be close to that of the material to be conveyed.
If cold air is used to convey a hot material, therefore, the cooling effect on the material of the cold air will be minimal. This is illustrated in more detail in Figure 9.20 where material and air inlet temperatures of 500°C and 20°C respectively have been considered.
Figure 9.20 is also drawn for a material having a specific heat of 1.0 kJ/kg K and highlights the influence of solids loading ratio. It must be stressed that the suspension of material and air will only reach the equilibrium temperature at some distance from the pipeline feeding point, for thermal transient effects have to be taken into account.
The heat transfer process depends additionally upon the thermal conductivity of the material and the shape and size of the particles.
It is a time dependent process and with the high velocities required in dilute phase conveying, equilibrium will not be fully established at the end of the pipeline with many materials. Since volumetric flow rate decreases with decrease in temperature, if there is any doubt with regard to the temperature of the air at the start of a conveying line, the lowest likely value should be used for design purposes.
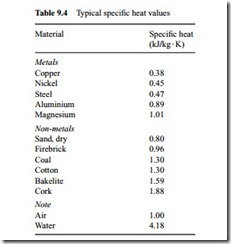
Specific heat
Specific heat is clearly an important property in this analysis and typical values are given in Table 9.4 for reference.
The specific heat values for air and water are also added for reference purposes, and that for air is a basic element in the model, of course. It will be noted, however, that water has a very much higher specific heat value than any of the other materials listed, and so if a material has a high moisture content this could have a considerable influence on the specific heat of the material.