NATURAL CONVECTION:NATURAL CONVECTION INSIDE ENCLOSURES

NATURAL CONVECTION INSIDE ENCLOSURES

A considerable portion of heat loss from a typical residence occurs through the windows. We certainly would insulate the windows, if we could, in order to conserve energy. The problem is finding an insulating material that is trans- parent. An examination of the thermal conductivities of the insulting materials reveals that air is a better insulator than most common insulating materials. Besides, it is transparent. Therefore, it makes sense to insulate the windows with a layer of air. Of course, we need to use another sheet of glass to trap the air. The result is an enclosure, which is known as a double-pane window in this case. Other examples of enclosures include wall cavities, solar collectors, and cryogenic chambers involving concentric cylinders or spheres. Enclosures are frequently encountered in practice, and heat transfer through them is of practical interest. Heat transfer in enclosed spaces is complicated by the fact that the fluid in the enclosure, in general, does not remain stationary. In a vertical enclosure, the fluid adjacent to the hotter surface rises and the luid adjacent to the cooler one falls, setting off a rotationary motion within the enclosure that enhances heat transfer through the enclosure. Typical flow patterns in vertical and horizontal rectangular enclosures are shown in Figs. 20–2l and 20–22.

The characteristics of heat transfer through a horizontal enclosure depend on whether the hotter plate is at the top or at the bottom, as shown in Fig. 20–22. When the hotter plate is at the top, no convection currents will de- velop in the enclosure, since the lighter fluid will always be on top of the heavier fluid. Heat transfer in this case will be by pure conduction, and we will have Nu = 1. When the hotter plate is at the bottom, the heavier fluid will be on top of the lighter fluid, and there will be a tendency for the lighter fluid to topple the heavier fluid and rise to the top, where it will come in contact with the cooler plate and cool down. Until that happens, however, the heat transfer is still by pure conduction and Nu = 1. When Ra > 1708, the buoy- ant force overcomes the fluid resistance and initiates natural convection cur- rents, which are observed to be in the form of hexagonal cells called Bénard cells. For Ra > 3 X 105, the cells break down and the fluid motion becomes turbulent.

The Rayleigh number for an enclosure is determined from

where T1 and T2 are the temperatures on the two sides of the layer. A comparison of this relation with Eq. 20–33 reveals that the convection heat transfer in an enclosure is analogous to heat conduction across the fluid layer in the en- closure provided that the thermal conductivity k is replaced by kNu. That is, the fluid in an enclosure behaves like a fluid whose thermal conductivity is kNu as a result of convection currents. Therefore, the quantity kNu is called the effective thermal conductivity of the enclosure. That is,

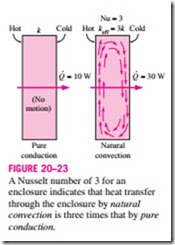
Note that for the special case of Nu = 1, the effective thermal conductivity of the enclosure becomes equal to the conductivity of the fluid. This is expected since this case corresponds to pure conduction (Fig. 20–23).

Natural convection heat transfer in enclosed spaces has been the subject of many experimental and numerical studies, and numerous correlations for the Nusselt number exist. Simple power-law type relations in the form of Nu = CRaL , where C and n are constants, are sufficiently accurate, but they are usually applicable to a narrow range of Prandtl and Rayleigh numbers and aspect ratios. The relations that are more comprehensive are naturally more complex. Next we present some widely used relations for various types of enclosures.

Horizontal Rectangular Enclosures

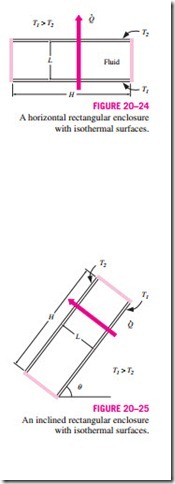
We need no Nusselt number relations for the case of the hotter plate being at the top, since there will be no convection currents in this case and heat trans- fer will be downward by conduction (Nu = 1). When the hotter plate is at the bottom, however, significant convection currents set in for RaL > 1708, and the rate of heat transfer increases (Fig. 20–24).

For horizontal enclosures that contain air, Jakob (1949) recommends the following simple correlations

These relations can also be used for other gases with 0.5 < Pr < 2. Using water, silicone oil, and mercury in their experiments, Globe and Dropkin (1959) obtained this correlation for horizontal enclosures heated from below,

The notation [ ]+ indicates that if the quantity in the bracket is negative, it should be set equal to zero. This relation also correlates data well for liquids with mod- erate Prandtl numbers for RaL < 105, and thus it can also be used for water.

Inclined Rectangular Enclosures

Air spaces between two inclined parallel plates are commonly encountered in flat-plate solar collectors (between the glass cover and the absorber plate) and the double-pane skylights on inclined roofs. Heat transfer through an inclined enclosure depends on the aspect ratio H/L as well as the tilt angle u from the horizontal (Fig. 20–25). H ·

For large aspect ratios (H/L 2: 12), this equation [Hollands et al., 1976] correlates experimental data extremely well for tilt angles up to 70°,

for RaL < 105, 0 < u < 70°, and H/L 2: 12. Again any quantity in [ ] should be set equal to zero if it is negative. This is to ensure that Nu = 1 for RaL cos u < 1708. Note that this relation reduces to Eq. 20–39 for horizontal enclosures for u = 0°, as expected.

Combined Natural Convection and Radiation

Gases are nearly transparent to radiation, and thus heat transfer through a gas layer is by simultaneous convection (or conduction, if the gas is quiescent) and radiation. Natural convection heat transfer coefficients are typically very low compared to those for forced convection. Therefore, radiation is usually disregarded in forced convection problems, but it must be considered in natural convection problems that involve a gas. This is especially the case for surfaces with high emissivities. For example, about half of the heat transfer through the air space of a double-pane window is by radiation. The total rate of heat transfer is determined by adding the convection and radiation components,

Radiation heat transfer from a surface at temperature Ts surrounded by surfaces at a temperature Tsurr (both in absolute temperature unit K) is determined from

When the end effects are negligible, radiation heat transfer between two large parallel plates at absolute temperatures T1 and T2 is expressed as (see Chap. 22 for details)

The emissivity of an ordinary glass surface, for example, is 0.84. Therefore, the effective emissivity of two parallel glass surfaces facing each other is 0.72. Radiation heat transfer between concentric cylinders and spheres is discussed in Chap. 22.

Note that in some cases the temperature of the surrounding medium may be below the surface temperature (TCX < Ts), while the temperature of the sur- rounding surfaces is above the surface temperature (Tsurr > Ts). In such cases, convection and radiation heat transfers are subtracted from each other instead of being added since they are in opposite directions. Also, for a metal surface, the radiation effect can be reduced to negligible levels by polishing the surface and thus lowering the surface emissivity to a value near zero.