FORCED CONVECTION: PHYSICAL MECHANISM OF CONVECTION

So far, we have considered conduction, which is the mechanism of heat transfer through a solid or fluid in the absence of any fluid motion. We now consider convection, which is the mechanism of heat transfer through a fluid in the presence of bulk fluid motion.

Convection is classified as natural (or free) or forced convection, depending on how the fluid motion is initiated. In forced convection, the fluid is forced to flow over a surface or in a pipe by external means such as a pump or a fan. In natural convection, any fluid motion is caused by natural means such as the buoyancy effect, which manifests itself as the rise of warmer fluid and the fall of the cooler fluid. Convection is also classified as external and internal, de- pending on whether the fluid is forced to flow over a surface or in a channel. We start this chapter with a general physical description of the convection mechanism and the thermal boundary layer. We continue with the discussion of the dimensionless Prandtl and Nusselt numbers, and their physical significance. We then present empirical relations for the heat transfer coefficients for flow over various geometries such as a flat plate, cylinder, and sphere, for both laminar and turbulent flow conditions. Finally, we discuss the characteristics of flow inside tubes and present the heat transfer correlations associated with it. The relevant concepts from Chaps. 14 and 15 should be reviewed before this chapter is studied.

■ PHYSICAL MECHANISM OF CONVECTION

We mentioned earlier that there are three basic mechanisms of heat transfer: conduction, convection, and radiation. Conduction and convection are similar in that both mechanisms require the presence of a material medium. But they are different in that convection requires the presence of fluid motion.

Heat transfer through a solid is always by conduction, since the molecules of a solid remain at relatively fixed positions. Heat transfer through a liquid or gas, however, can be by conduction or convection, depending on the presence of any bulk fluid motion. Heat transfer through a fluid is by convection in the presence of bulk fluid motion and by conduction in the absence of it. There- fore, conduction in a fluid can be viewed as the limiting case of convection, corresponding to the case of quiescent fluid (Fig. 19–1).

Convection heat transfer is complicated by the fact that it involves fluid motion as well as heat conduction. The fluid motion enhances heat transfer, since it brings hotter and cooler chunks of fluid into contact, initiating higher rates of conduction at a greater number of sites in a fluid. Therefore, the rate of heat transfer through a fluid is much higher by convection than it is by conduction. In fact, the higher the fluid velocity, the higher the rate of heat transfer.

To clarify this point further, consider steady heat transfer through a fluid contained between two parallel plates maintained at different temperatures, as shown in Fig. 19–2. The temperatures of the fluid and the plate will be the same at the points of contact because of the continuity of temperature. Assuming no fluid motion, the energy of the hotter fluid molecules near the hot plate will be transferred to the adjacent cooler fluid molecules. This energy will then be transferred to the next layer of the cooler fluid molecules. This energy will then be transferred to the next layer of the cooler fluid, and so on, until it is finally transferred to the other plate. This is what happens during conduction through a fluid. Now let us use a syringe to draw some fluid near the hot plate and inject it near the cold plate repeatedly. You can imagine that this will speed up the heat transfer process considerably, since some energy is Consider the cooling of a hot iron block with a fan blowing air over its top surface, as shown in Fig. 19–3. We know that heat will be transferred from the hot block to the surrounding cooler air, and the block will eventually cool. We also know that the block will cool faster if the fan is switched to a higher speed. Replacing air by water will enhance the convection heat transfer even more.

Experience shows that convection heat transfer strongly depends on the fluid properties dynamic viscosity m, thermal conductivity k, density r, and specific heat Cp, as well as the fluid velocity ‘V. It also depends on the geometry and the roughness of the solid surface, in addition to the type of fluid flow (such as being streamlined or turbulent). Thus, we expect the convection heat transfer relations to be rather complex because of the dependence of convection on so many variables. This is not surprising, since convection is the most complex mechanism of heat transfer.

Despite the complexity of convection, the rate of convection heat transfer is observed to be proportional to the temperature difference and is conveniently expressed by Newton’s law of cooling as Judging from its units, the convection heat transfer coefficient h can be de- fined as the rate of heat transfer between a solid surface and a fluid per unit surface area per unit temperature difference.

You should not be deceived by the simple appearance of this relation, be- cause the convection heat transfer coefficient h depends on several of the mentioned variables, and thus is difficult to determine.

When a fluid is forced to flow over a solid surface that is nonporous (i.e., impermeable to the fluid), it is observed that the fluid in motion comes to a complete stop at the surface and assumes a zero velocity relative to the surface. That is, the fluid layer in direct contact with a solid surface “sticks” to the surface and there is no slip. In fluid flow, this phenomenon is known as the no-slip condition, and it is due to the viscosity of the fluid (Fig. 19–4).

The no-slip condition is responsible for the development of the velocity profile for flow. Because of the friction between the fluid layers, the layer that sticks to the wall slows the adjacent fluid layer, which slows the next layer, and so on. A consequence of the no-slip condition is that all velocity profiles must have zero values at the points of contact between a fluid and a solid. The only exception to the no-slip condition occurs in extremely rarified gases. A similar phenomenon occurs for the temperature. When two bodies at different temperatures are brought into contact, heat transfer occurs until both bodies assume the same temperature at the point of contact. Therefore, a fluid and a solid surface will have the same temperature at the point of contact. This is known as no-temperature-jump condition.

An implication of the no-slip and the no-temperature-jump conditions is that heat transfer from the solid surface to the fluid layer adjacent to the surface is by pure conduction, since the fluid layer is motionless, and can be expressed as

where T represents the temperature distribution in the fluid and (aT/ay)y=0 is the temperature gradient at the surface. This heat is then convected away from the surface as a result of fluid motion. Note that convection heat transfer from a solid surface to a fluid is merely the conduction heat transfer from the solid surface to the fluid layer adjacent to the surface. Therefore, we can equate Eqs. 19–1 and 19–3 for the heat flux to obtain

for the determination of the convection heat transfer coefficient when the temperature distribution within the fluid is known.

The convection heat transfer coefficient, in general, varies along the flow (or x-) direction. The average or mean convection heat transfer coefficient for a surface in such cases is determined by properly averaging the local convection heat transfer coefficients over the entire surface as

Nusselt Number

In convection studies, it is common practice to nondimensionalize the governing equations and combine the variables, which group together into di- mensionless numbers in order to reduce the number of total variables. It is also common practice to nondimensionalize the heat transfer coefficient h with the Nusselt number, defined as

where k is the thermal conductivity of the fluid and Lc is the characteristic length. The Nusselt number is named after Wilhelm Nusselt, who made significant contributions to convective heat transfer in the first half of the twentieth century, and it is viewed as the dimensionless convection heat transfer coefficient.

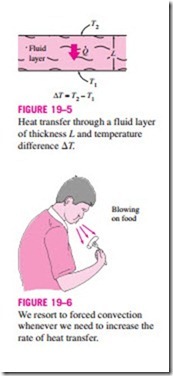
To understand the physical significance of the Nusselt number, consider a fluid layer of thickness L and temperature difference !JT = T2 – T1, as shown in Fig. 19–5. Heat transfer through the fluid layer will be by convection when the fluid involves some motion and by conduction when the fluid layer is motionless. Heat flux (the rate of heat transfer per unit time per unit surface area) in either case will be

which is the Nusselt number. Therefore, the Nusselt number represents the enhancement of heat transfer through a fluid layer as a result of convection relative to conduction across the same fluid layer. The larger the Nusselt number, the more effective the convection. A Nusselt number of Nu = 1 for a fluid layer represents heat transfer across the layer by pure conduction.

We use forced convection in daily life more often than you might think (Fig. 19–6). We resort to forced convection whenever we want to increase the rate of heat transfer from a hot object. For example, we turn on the fan on hot summer days to help our body cool more effectively. The higher the fan speed, the better we feel. We stir our soup and blow on a hot slice of pizza to make them cool faster. The air on windy winter days feels much colder than it actually is. The simplest solution to heating problems in electronics packaging is to use a large enough fan.