So far, we have considered various forms of energy such as heat Q, work W, and total energy E individually, and no attempt has been made to relate them to each other during a process. The first law of thermodynamics, also known as the conservation of energy principle, provides a sound basis for studying the relationships among the various forms of energy and energy interactions. Based on experimental observations, the first law of thermodynamics states that energy can be neither created nor destroyed; it can only change forms. Therefore, every bit of energy should be accounted for during a process.
We all know that a rock at some elevation possesses some potential energy, and part of this potential energy is converted to kinetic energy as the rock falls (Fig. 5–1). Experimental data show that the decrease in potential energy (mg�z) exactly equals the increase in kinetic energy [m(‘V2 – ‘V2)/2] when the air resistance is negligible, thus confirming the conservation of energy principle.
Consider a system undergoing a series of adiabatic processes from a specified state 1 to another specified state 2. Being adiabatic, these processes obvi- ously cannot involve any heat transfer, but they may involve several kinds of work interactions. Careful measurements during these experiments indicate the following: For all adiabatic processes between two specified states of a closed system, the net work done is the same regardless of the nature of the closed system and the details of the process. Considering that there are an infinite number of ways to perform work interactions under adiabatic conditions, this statement appears to be very powerful, with a potential for far- reaching implications. This statement, which is largely based on the experiments of Joule in the first half of the nineteenth century, cannot be drawn from any other known physical principle and is recognized as a funda- mental principle. This principle is called the first law of thermodynamics or just the first law.
A major consequence of the first law is the existence and the definition of the property total energy E. Considering that the net work is the same for all adiabatic processes of a closed system between two specified states, the value of the net work must depend on the end states of the system only, and thus it must correspond to a change in a property of the system. This property is the total energy. Note that the first law makes no reference to the value of the total energy of a closed system at a state. It simply states that the change in the total energy during an adiabatic process must be equal to the net work done. There- fore, any convenient arbitrary value can be assigned to total energy at a speci- fied state to serve as a reference point.
Implicit in the first law statement is the conservation of energy. Although the essence of the first law is the existence of the property total energy, the first law is often viewed as a statement of the conservation of energy prin- ciple. Next we develop the first law or the conservation of energy relation for closed systems with the help of some familiar examples using intuitive arguments.
First, we consider some processes that involve heat transfer but no work interactions. The potato baked in the oven is a good example for this case (Fig. 5–2). As a result of heat transfer to the potato, the energy of the potato will increase. If we disregard any mass transfer (moisture loss from the potato), the increase in the total energy of the potato becomes equal to the amount of heat transfer. That is, if 5 kJ of heat is transferred to the potato, the energy increase of the potato will also be 5 kJ.
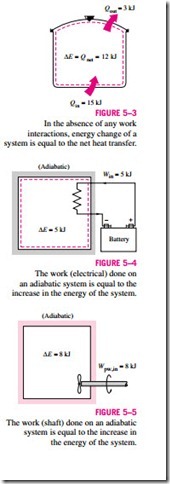
As another example, consider the heating of water in a pan on top of a range (Fig. 5–3). If 15 kJ of heat is transferred to the water from the heating element and 3 kJ of it is lost from the water to the surrounding air, the increase in energy of the water will be equal to the net heat transfer to water, which is 12 kJ.
Now consider a well-insulated (i.e., adiabatic) room heated by an electric heater as our system (Fig. 5–4). As a result of electrical work done, the energy of the system will increase. Since the system is adiabatic and cannot have any heat transfer to or from the surroundings (Q = 0), the conservation of energy principle dictates that the electrical work done on the system must equal the increase in energy of the system.
Next, let us replace the electric heater with a paddle wheel (Fig. 5–5). As a result of the stirring process, the energy of the system will increase. Again, since there is no heat interaction between the system and its surroundings (Q = 0), the paddle-wheel work done on the system must show up as an in- crease in the energy of the system.
Many of you have probably noticed that the temperature of air rises when it form of boundary work. In the absence of any heat transfer (Q = 0), the entire boundary work will be stored in the air as part of its total energy. The conservation of energy principle again requires that the increase in the energy of the system be equal to the boundary work done on the system.
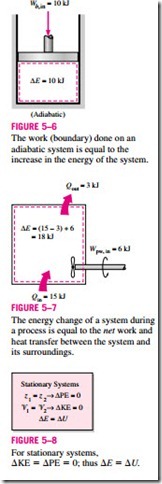
We can extend these discussions to systems that involve various heat and work interactions simultaneously. For example, if a system gains 12 kJ of heat during a process while 6 kJ of work is done on it, the increase in the energy of the system during that process is 18 kJ (Fig. 5–7). That is, the change in the energy of a system during a process is simply equal to the net energy transfer to (or from) the system.
Energy Balance
In the light of the preceding discussions, the conservation of energy principle can be expressed as follows: The net change (increase or decrease) in the total energy of the system during a process is equal to the difference between the total energy entering and the total energy leaving the system during that process. That is, during a process,
This relation is often referred to as the energy balance and is applicable to any kind of system undergoing any kind of process. The successful use of this relation to solve engineering problems depends on understanding the various forms of energy and recognizing the forms of energy transfer.
Energy Change of a System
The determination of the energy change of a system during a process involves the evaluation of the energy of the system at the beginning and at the end of the process, and taking their difference. That is,
Energy change = Energy at final state – Energy at initial state
Note that energy is a property, and the value of a property does not change un- less the state of the system changes. Therefore, the energy change of a system is zero if the state of the system does not change during the process. Also, energy can exist in numerous forms such as internal (sensible, latent, chemical, and nuclear), kinetic, potential, electric, and magnetic, and their sum constitutes the total energy E of a system. In the absence of electric, magnetic, and surface tension effects (i.e., for simple compressible systems), the change in the total energy of a system during a process is the sum of the changes in its internal, kinetic, and potential energies and can be expressed as
When the initial and final states are specified, the values of the specific internal energies u1 and u2 can be determined directly from the property tables or thermodynamic property relations.
Most systems encountered in practice are stationary, that is, they do not involve any changes in their velocity or elevation during a process (Fig. 5–8). Thus, for stationary systems, the changes in kinetic and potential energies are zero (that is, �KE = �PE = 0), and the total energy change relation in Eq. 5–2 reduces to �E = �U for such systems. Also, the energy of a system during a process will change even if only one form of its energy changes while the other forms of energy remain unchanged.
Mechanisms of Energy Transfer, Ein and Eout
Energy can be transferred to or from a system in three forms: heat, work, and mass flow. Energy interactions are recognized at the system boundary as they cross it, and they represent the energy gained or lost by a system during a process. The only two forms of energy interactions associated with a fixed mass or closed system are heat transfer and work.
1. Heat Transfer, Q Heat transfer to a system (heat gain) increases the en- ergy of the molecules and thus the internal energy of the system, and heat transfer from a system (heat loss) decreases it since the energy transferred out as heat comes from the energy of the molecules of the system.
2. Work, W An energy interaction that is not caused by a temperature difference between a system and its surroundings is work. A rising piston, a rotating shaft, and an electrical wire crossing the system boundaries are all associated with work interactions. Work transfer to a system (i.e., work done on a system) increases the energy of the system, and work transfer from a system (i.e., work done by the system) decreases it since the energy transferred out as work comes from the energy contained in the system. Car engines and hydraulic, steam, or gas turbines produce work while compressors, pumps, and mixers consume work.
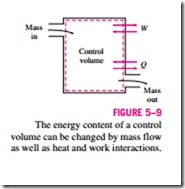
3. Mass Flow, m Mass flow in and out of the system serves as an additional mechanism of energy transfer. When mass enters a system, the energy of the system increases because mass carries energy with it (in fact, mass is energy). Likewise, when some mass leaves the system, the energy contained within the system decreases because the leaving mass takes out some energy with it. For example, when some hot water is taken out of a water heater and is replaced by the same amount of cold water, the energy content of the hot- water tank (the control volume) decreases as a result of this mass interaction (Fig. 5–9).
Noting that energy can be transferred in the forms of heat, work, and mass, and that the net transfer of a quantity is equal to the difference between the amounts transferred in and out, the energy balance can be written more ex- plicitly as
where the subscripts “in’’ and “out’’ denote quantities that enter and leave the system, respectively. All six quantities on the right side of the equation rep- resent “amounts,’’ and thus they are positive quantities. The direction of any energy transfer is described by the subscripts “in’’ and “out.’’ Therefore, we do not need to adopt a formal sign convention for heat and work interactions. When heat or work is to be determined and their direction is unknown, we can assume any direction (in or out) for heat or work and solve the problem. A negative result in that case will indicate that the assumed direction is wrong, and it is corrected by reversing the assumed direction. This is just like assum- ing a direction for an unknown force when solving a problem in statics and reversing the assumed direction when a negative quantity is obtained.
The heat transfer Q is zero for adiabatic systems, the work transfer W is zero for systems that involve no work interactions, and the energy transport with mass Emass is zero for systems that involve no mass flow across their bound- aries (i.e., closed systems).
Energy balance for any system undergoing any kind of process can be ex- pressed more compactly as
The energy balance can be expressed on a per unit mass basis as
Incoming search terms:
- what are the only two forms of energy interactions associated with a closed system
- the increase in the energy of a potato in the oven is equal to the amount of heat transferred to it
- two forms of energy interactions associated with a closed system
- what are only two forms of energy interaction associated with close system
- What are the only two forms of energy interactions associated with a closed system?
- What law asserts that energy is a themodynamic property?
- Which of the following property changes when a potato is baked in an oven? Internal energy Enthalpy