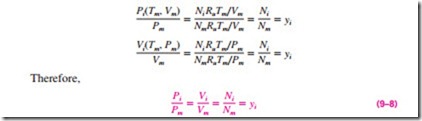■ P-v-T BEHAVIOR OF GAS MIXTURES: IDEAL AND REAL GASES
An ideal gas is defined as a gas whose molecules are spaced far apart so that the behavior of a molecule is not influenced by the presence of other molecules—a situation encountered at low densities. We also mentioned that real gases approximate this behavior closely when they are at a low pressure or high temperature relative to their critical-point values. The P-υ-T behavior of an ideal gas is expressed by the simple relation Pυ = RT, which is called the ideal-gas equation of state. The P-υ-T behavior of real gases is expressed by more complex equations of state or by Pυ = ZRT, where Z is the compressibility factor.
When two or more ideal gases are mixed, the behavior of a molecule normally is not influenced by the presence of other similar or dissimilar molecules, and therefore a nonreacting mixture of ideal gases also behaves as an ideal gas. Air, for example, is conveniently treated as an ideal gas in the range where nitrogen and oxygen behave as ideal gases. When a gas mixture consists of real (nonideal) gases, however, the prediction of the P-υ-T behavior of the mixture becomes rather involved.
The prediction of the P-υ-T behavior of gas mixtures is usually based on two models: Dalton’s law of additive pressures and Amagat’s law of additive volumes. Both models are described and discussed below.
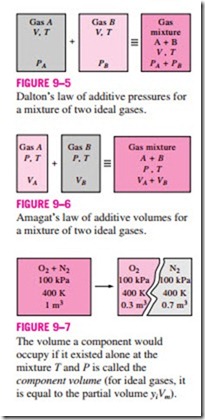
Dalton’s law of additive pressures: The pressure of a gas mixture is equal to the sum of the pressures each gas would exert if it existed alone at the mixture temperature and volume (Fig. 9–5).
Amagat’s law of additive volumes: The volume of a gas mixture is equal to the sum of the volumes each gas would occupy if it existed alone at the mixture temperature and pressure (Fig. 9–6).
Dalton’s and Amagat’s laws hold exactly for ideal-gas mixtures, but only approximately for real-gas mixtures. This is due to intermolecular forces that may be significant for real gases at high densities. For ideal gases, these two laws are identical and give identical results.
Dalton’s and Amagat’s laws can be expressed as follows:
In these relations, Pi is called the component pressure and Vi is called the component volume (Fig. 9–7). Note that Vi is the volume a component would occupy if it existed alone at Tm and Pm, not the actual volume occupied by the The volume a component would occupy if it existed alone at the mixture T and P is called the component volume (for ideal gases, it is equal to the partial volume yiVm).
component in the mixture. (In a vessel that holds a gas mixture, each component fills the entire volume of the vessel. Therefore, the volume of each component is equal to the volume of the vessel.) Also, the ratio Pi /Pm is called the pressure fraction and the ratio Vi /Vm is called the volume fraction of component i.
Ideal-Gas Mixtures
For ideal gases, Pi and Vi can be related to yi by using the ideal-gas relation for both the components and the gas mixture:
Equation 9–8 is strictly valid for ideal-gas mixtures since it is derived by assuming ideal-gas behavior for the gas mixture and each of its components. The quantity yiPm is called the partial pressure (identical to the component pressure for ideal gases), and the quantity yiVm is called the partial volume (identical to the component volume for ideal gases). Note that for an ideal-gas mixture, the mole fraction, the pressure fraction, and the volume fraction of a component are identical.
The composition of an ideal-gas mixture (such as the exhaust gases leaving a combustion chamber) is frequently determined by a volumetric analysis (called the Orsat Analysis) and Eq. 9–8. A sample gas at a known volume, pressure, and temperature is passed into a vessel containing reagents that absorb one of the gases. The volume of the remaining gas is then measured at the original pressure and temperature. The ratio of the reduction in volume to the original volume (volume fraction) represents the mole fraction of that particular gas.
Real-Gas Mixtures
Dalton’s law of additive pressures and Amagat’s law of additive volumes can also be used for real gases, often with reasonable accuracy. This time, how- ever, the component pressures or component volumes should be evaluated from relations that take into account the deviation of each component from ideal-gas behavior. One way of doing that is to use more exact equations of state (van der Waals, Beattie–Bridgeman, Benedict–Webb–Rubin, etc.) in- stead of the ideal-gas equation of state. Another way is to use the compressibility factor (Fig. 9–8) as
where Zi is determined either at Tm and Vm (Dalton’s law) or at Tm and Pm (Amagat’s law) for each individual gas. It may seem that using either law will give the same result, but it does not.
The compressibility-factor approach, in general, gives more accurate results when the Zi’s in Eq. 9–10 are evaluated by using Amagat’s law instead of Dalton’s law. This is because Amagat’s law involves the use of mixture pressure Pm, which accounts for the influence of intermolecular forces between the molecules of different gases. Dalton’s law disregards the influence of dissimilar molecules in a mixture on each other. As a result, it tends to underpredict the pressure of a gas mixture for a given Vm and Tm. Therefore, Dalton’s law is more appropriate for gas mixtures at low pressures. Amagat’s law is more appropriate at high pressures.
Note that there is a significant difference between using the compressibility factor for a single gas and for a mixture of gases. The compressibility factor predicts the P-υ-T behavior of single gases rather accurately, as discussed in Chap. 3, but not for mixtures of gases. When we use compressibility factors for the components of a gas mixture, we account for the influence of like molecules on each other; the influence of dissimilar molecules remains largely unaccounted for. Consequently, a property value predicted by this approach may be considerably different from the experimentally determined value.