ENTROPY:ISENTROPIC EFFICIENCIES OF STEADY-FLOW DEVICES

■ ISENTROPIC EFFICIENCIES OF STEADY-FLOW DEVICES

We mentioned repeatedly that irreversibilities inherently accompany all actual processes and that their effect is always to downgrade the performance of devices. In engineering analysis, it would be very desirable to have some parameters that would enable us to quantify the degree of degradation of energy in these devices. In the last chapter we did this for cyclic devices, such as heat engines and refrigerators, by comparing the actual cycles to the idealized ones, such as the Carnot cycle. A cycle that was composed entirely of reversible processes served as the model cycle to which the actual cycles could be compared. This idealized model cycle enabled us to determine the theoretical limits of performance for cyclic devices under specified conditions and to examine how the performance of actual devices suffered as a result of irreversibilities.

Now we extend the analysis to discrete engineering devices working under steady-flow conditions, such as turbines, compressors, and nozzles, and we examine the degree of degradation of energy in these devices as a result of irreversibilities. However, first we need to define an ideal process that will serve as a model for the actual processes.

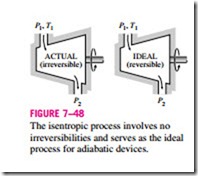
Although some heat transfer between these devices and the surrounding medium is unavoidable, many steady-flow devices are intended to operate under adiabatic conditions. Therefore, the model process for these devices should be an adiabatic one. Furthermore, an ideal process should involve no irreversibilities since the effect of irreversibilities is always to downgrade the performance of engineering devices. Thus, the ideal process that can serve as a suitable model for adiabatic steady-flow devices is the isentropic process (Fig. 7–48).

The more closely the actual process approximates the idealized isentropic process, the better the device will perform. Thus, it would be desirable to have a parameter that expresses quantitatively how efficiently an actual device approximates an idealized one. This parameter is the isentropic or adiabatic efficiency, which is a measure of the deviation of actual processes from the corresponding idealized ones.

Isentropic efficiencies are defined differently for different devices since each device is set up to perform different tasks. Next we define the isentropic efficiencies of turbines, compressors, and nozzles by comparing the actual performance of these devices to their performance under isentropic conditions for the same inlet state and exit pressure.

Isentropic Efficiency of Turbines

For a turbine under steady operation, the inlet state of the working fluid and the exhaust pressure are fixed. Therefore, the ideal process for an adiabatic turbine is an isentropic process between the inlet state and the exhaust pressure. The desired output of a turbine is the work produced, and the isentropic efficiency of a turbine is defined as the ratio of the actual work output of the turbine to the work output that would be achieved if the process between the inlet state and the exit pressure were isentropic:

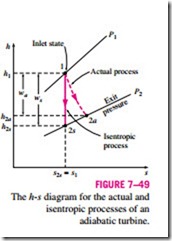
Usually the changes in kinetic and potential energies associated with a fluid stream flowing through a turbine are small relative to the change in enthalpy and can be neglected. Then the work output of an adiabatic turbine simply becomes the change in enthalpy, and Eq. 7–60 becomes

where h2a and h2s are the enthalpy values at the exit state for actual and isentropic processes, respectively (Fig. 7–49).

The value of hT greatly depends on the design of the individual components that make up the turbine. Well-designed, large turbines have isentropic efficiencies above 90 percent. For small turbines, however, it may drop even below 70 percent. The value of the isentropic efficiency of a turbine is deter- mined by measuring the actual work output of the turbine and by calculating the isentropic work output for the measured inlet conditions and the exit pressure. This value can then be used conveniently in the design of power plants.

Isentropic Efficiencies of Compressors and Pumps

The isentropic efficiency of a compressor is defined as the ratio of the work input required to raise the pressure of a gas to a specified value in an isentropic manner to the actual work input:

Notice that the isentropic compressor efficiency is defined with the isentropic work input in the numerator instead of in the denominator. This is because ws is a smaller quantity than wa, and this definition prevents hC from becoming greater than 100 percent, which would falsely imply that the actual compressors performed better than the isentropic ones. Also notice that the inlet conditions and the exit pressure of the gas are the same for both the actual and the isentropic compressor.

When the changes in kinetic and potential energies of the gas being com- pressed are negligible, the work input to an adiabatic compressor becomes

where h2a and h2s are the enthalpy values at the exit state for actual and isentropic compression processes, respectively, as illustrated in Fig. 7–51.

Again, the value of hC greatly depends on the design of the compressor. Well- designed compressors have isentropic efficiencies that range from 75 to 85 percent.

When the changes in potential and kinetic energies of a liquid are negligible, the isentropic efficiency of a pump is defined similarly as

When no attempt is made to cool the gas as it is compressed, the actual compression process is nearly adiabatic and the reversible adiabatic (i.e., isentropic) process serves well as the ideal process. However, sometimes compressors are cooled intentionally by utilizing fins or a water jacket placed around the casing to reduce the work input requirements (Fig. 7–52). In this case, the isentropic process is not suitable as the model process since the device is no longer adiabatic and the isentropic compressor efficiency defined above is meaningless. A realistic model process for compressors that are intentionally cooled during the compression process is the reversible isothermal process. Then we can conveniently define an isothermal efficiency for such cases by comparing the actual process to a reversible isothermal one:

where wt and wa are the required work inputs to the compressor for the reversible isothermal and actual cases, respectively.

Isentropic Efficiency of Nozzles

Nozzles are essentially adiabatic devices and are used to accelerate a fluid.

Therefore, the isentropic process serves as a suitable model for nozzles. The isentropic efficiency of a nozzle is defined as the ratio of the actual kinetic energy of the fluid at the nozzle exit to the kinetic energy value at the exit of an isentropic nozzle for the same inlet state and exit pressure. That is,

Note that the exit pressure is the same for both the actual and isentropic processes, but the exit state is different.

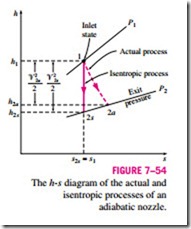
Nozzles involve no work interactions, and the fluid experiences little or no change in its potential energy as it flows through the device. If, in addition, the h inlet velocity of the fluid is small relative to the exit velocity, the energy balance for this steady-flow device reduces to

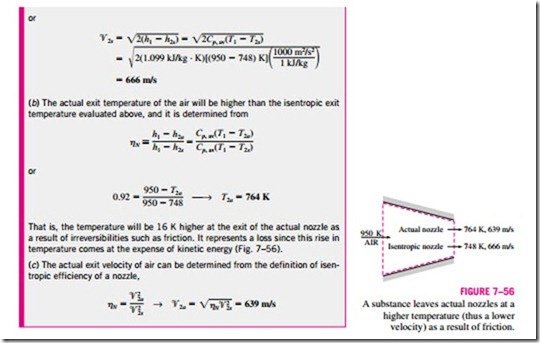
where h2a and h2s are the enthalpy values at the nozzle exit for the actual and isentropic processes, respectively (Fig. 7–54). Isentropic efficiencies of nozzles are typically above 90 percent, and nozzle efficiencies above 95 percent are not uncommon.