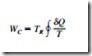ENTROPY

In Chap. 6, we introduced the second law of thermodynamics and applied it to cycles and cyclic devices. In this chapter, we apply the second law to processes. The first law of thermodynamics deals with the property energy and the conservation of it. The second law leads to the definition of a new property called entropy. Entropy is a somewhat abstract property, and it is difficult to give a physical description of it without considering the microscopic state of the system. Entropy is best understood and appreciated by studying its uses in commonly encountered engineering processes, and this is what we intend to do.

This chapter starts with a discussion of the Clausius inequality, which forms the basis for the definition of entropy, and continues with the increase of entropy principle. Unlike energy, entropy is a nonconserved property, and there is no such thing as a conservation of entropy principle. Next, the entropy changes that take place during processes for pure substances, in- compressible substances, and ideal gases are discussed, and a special class of idealized processes, called isentropic processes, is examined. Then, the reversible steady-flow work and the isentropic efficiencies of various engineering devices such as turbines and compressors are considered. Finally, entropy balance is introduced and applied to various systems.

ENTROPY

The second law of thermodynamics often leads to expressions that involve in- equalities. An irreversible (i.e., actual) heat engine, for example, is less efficient than a reversible one operating between the same two thermal energy reservoirs. Likewise, an irreversible refrigerator or a heat pump has a lower coefficient of performance (COP) than a reversible one operating between the same temperature limits. Another important inequality that has major consequences in thermodynamics is the Clausius inequality. It was first stated by the German physicist R. J. E. Clausius (1822–1888), one of the founders of thermodynamics, and is expressed as

That is, the cyclic integral of dQ/T is always less than or equal to zero. This inequality is valid for all cycles, reversible or irreversible. The symbol 9 (integral symbol with a circle in the middle) is used to indicate that the integration is to be performed over the entire cycle. Any heat transfer to or from a system can be considered to consist of differential amounts of heat transfer. Then the cyclic integral of dQ/T can be viewed as the sum of all these differential amounts of heat transfer divided by the absolute temperature at the boundary.

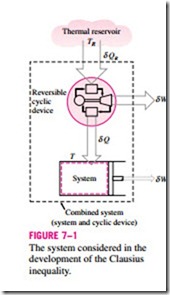
To demonstrate the validity of the Clausius inequality, consider a system connected to a thermal energy reservoir at a constant absolute temperature of TR through a reversible cyclic device (Fig. 7–1). The cyclic device receives heat dQR from the reservoir and supplies heat dQ to the system whose ab- solute temperature at that part of the boundary is T (a variable) while producing work dWrev. The system produces work dWsys as a result of this heat transfer. Applying the energy balance to the combined system identified by dashed lines yields

where dWC is the total work of the combined system (dWrev + dWsys) and dEC is the change in the total energy of the combined system. Considering that the cyclic device is a reversible one, we have

where the sign of dQ is determined with respect to the system (positive if to the system and negative if from the system) and the sign of dQR is determined with respect to the reversible cyclic device. Eliminating dQR from the two relations above yields

We now let the system undergo a cycle while the cyclic device undergoes an integral number of cycles. Then the preceding relation becomes

since the cyclic integral of energy (the net change in the energy, which is a property, during a cycle) is zero. Here WC is the cyclic integral of dWC, and it represents the net work for the combined cycle.

It appears that the combined system is exchanging heat with a single thermal energy reservoir while involving (producing or consuming) work WC during a cycle. On the basis of the Kelvin–Planck statement of the second law, which states that no system can produce a net amount of work while operating in a cycle and exchanging heat with a single thermal energy reservoir, we reason that WC cannot be a work output, and thus it cannot be a positive quantity. Considering that TR is an absolute temperature and thus a positive quantity, we must have

which is the Clausius inequality. This inequality is valid for all thermo- dynamic cycles, reversible or irreversible, including the refrigeration cycles. If no irreversibilities occur within the system as well as the reversible cyclic device, then the cycle undergone by the combined system will be internally reversible. As such, it can be reversed. In the reversed cycle case, all the quantities will have the same magnitude but the opposite sign. Therefore, the work WC, which could not be a positive quantity in the regular case, cannot be a negative quantity in the reversed case. Then it follows that WC, int rev = 0 since it cannot be a positive or negative quantity, and therefore

for internally reversible cycles. Thus, we conclude that the equality in the Clausius inequality holds for totally or just internally reversible cycles and the inequality for the irreversible ones.

To develop a relation for the definition of entropy, let us examine Eq. 7–2 more closely. Here we have a quantity whose cyclic integral is zero. Let us think for a moment what kind of quantities can have this characteristic. We know that the cyclic integral of work is not zero. (It is a good thing that it is not. Otherwise, heat engines that work on a cycle such as steam power plants would produce zero net work.) Neither is the cyclic integral of heat.

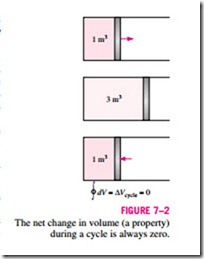
Now consider the volume occupied by a gas in a piston-cylinder device undergoing a cycle, as shown in Fig. 7–2. When the piston returns to its initial position at the end of a cycle, the volume of the gas also returns to its initial value. Thus the net change in volume during a cycle is zero. This is also ex- pressed as

That is, the cyclic integral of volume (or any other property) is zero. Conversely, a quantity whose cyclic integral is zero depends on the state only and not the process path, and thus it is a property. Therefore, the quantity (dQ/T)int rev must represent a property in the differential form.

Clausius realized in 1865 that he had discovered a new thermodynamic property, and he chose to name this property entropy. It is designated S and is defined as

Entropy is an extensive property of a system and sometimes is referred to as total entropy. Entropy per unit mass, designated s, is an intensive property and has the unit kJ/kg · K. The term entropy is generally used to refer to both total entropy and entropy per unit mass since the context usually clarifies which one is meant.

The entropy change of a system during a process can be determined by integrating Eq. 7–4 between the initial and the final states:

Notice that we have actually defined the change in entropy instead of entropy itself, just as we defined the change in energy instead of the energy itself when we developed the first-law relation. Absolute values of entropy are determined on the basis of the third law of thermodynamics, which is discussed later in this chapter. Engineers are usually concerned with the changes in entropy. Therefore, the entropy of a substance can be assigned a zero value at some arbitrarily selected reference state, and the entropy values at other states can be determined from Eq. 7–5 by choosing state 1 to be the reference state (S = 0) and state 2 to be the state at which entropy is to be determined.

To perform the integration in Eq. 7–5, one needs to know the relation be- tween Q and T during a process. This relation is often not available, and the integral in Eq. 7–5 can be performed for a few cases only. For the majority of cases we have to rely on tabulated data for entropy.

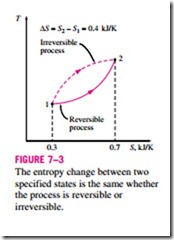
Note that entropy is a property, and like all other properties, it has fixed values at fixed states. Therefore, the entropy change !::S between two specified states is the same no matter what path, reversible or irreversible, is followed during a process (Fig. 7–3).

Also note that the integral of dQ/T will give us the value of entropy change only if the integration is carried out along an internally reversible path between the two states. The integral of dQ/T along an irreversible path is not a property, and in general, different values will be obtained when the integration is carried out along different irreversible paths. Therefore, even for irreversible processes, the entropy change should be determined by carrying out this integration along some convenient imaginary internally reversible path between the specified states.

A Special Case: Internally Reversible Isothermal Heat Transfer Processes

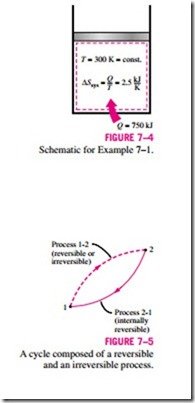
Recall that isothermal heat transfer processes are internally reversible. There-fore, the entropy change of a system during an internally reversible isothermal

heat transfer process can be determined by performing the integration in Eq. 7–5:

where T0 is the constant absolute temperature of the system and Q is the heat transfer for the internally reversible process. Equation 7–6 is particularly useful for determining the entropy changes of thermal energy reservoirs that can absorb or supply heat indefinitely at a constant temperature.

Notice that the entropy change of a system during an internally reversible isothermal process can be positive or negative, depending on the direction of heat transfer. Heat transfer to a system will increase the entropy of a system, whereas heat transfer from a system will decrease it. In fact, losing heat is the only way the entropy of a system can be decreased.