FORMS OF ENERGY
Energy can exist in numerous forms such as thermal, mechanical, kinetic, potential, electric, magnetic, chemical, and nuclear, and their sum constitutes the total energy E of a system. The total energy of a system on a unit mass basis is denoted by e and is defined as
Thermodynamics provides no information about the absolute value of the total energy. It deals only with the change of the total energy, which is what matters in engineering problems. Thus the total energy of a system can be as- signed a value of zero (E = 0) at some convenient reference point. The change in total energy of a system is independent of the reference point selected. The decrease in the potential energy of a falling rock, for example, depends on only the elevation difference and not the reference level selected.
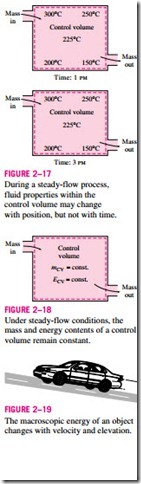
In thermodynamic analysis, it is often helpful to consider the various forms of energy that make up the total energy of a system in two groups: macro-
Under steady-flow conditions, the mass and energy contents of a control volume remain constant.
possesses as a whole with respect to some outside reference frame, such as kinetic and potential energies (Fig. 2–19). The microscopic forms of energy are those related to the molecular structure of a system and the degree of the molecular activity, and they are independent of outside reference frames. The sum of all the microscopic forms of energy is called the internal energy of a sys- tem and is denoted by U.
The term energy was coined in 1807 by Thomas Young, and its use in thermodynamics was proposed in 1852 by Lord Kelvin. The term internal energy and its symbol U first appeared in the works of Rudolph Clausius and William Rankine in the second half of the nineteenth century, and it eventually re- placed the alternative terms inner work, internal work, and intrinsic energy commonly used at the time.
The macroscopic energy of a system is related to motion and the influence of some external effects such as gravity, magnetism, electricity, and surface tension. The energy that a system possesses as a result of its motion relative to some reference frame is called kinetic energy KE. When all parts of a system move with the same velocity, the kinetic energy is expressed as
Most closed systems remain stationary during a process and thus experience no change in their kinetic and potential energies. Closed systems whose ve- locity and elevation of the center of gravity remain constant during a process are frequently referred to as stationary systems. The change in the total energy /1E of a stationary system is identical to the change in its internal energy /1U. In this text, a closed system is assumed to be stationary unless it is specifically stated otherwise.
Some Physical Insight to Internal Energy
Internal energy is defined earlier as the sum of all the microscopic forms of energy of a system. It is related to the molecular structure and the degree of molecular activity and can be viewed as the sum of the kinetic and potential energies of the molecules.
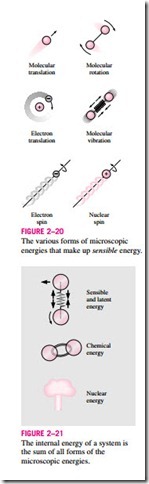
To have a better understanding of internal energy, let us examine a system at the molecular level. The molecules of a gas move through space with some velocity, and thus possess some kinetic energy. This is known as the translational energy. The atoms of polyatomic molecules rotate about an axis, and the energy associated with this rotation is the rotational kinetic energy. The atoms of a polyatomic molecule may also vibrate about their common center of mass, and the energy associated with this back-and-forth motion is the vibrational kinetic energy. For gases, the kinetic energy is mostly due to translational and rotational motions, with vibrational motion becoming significant at higher temperatures. The electrons in an atom rotate about the nucleus, and thus possess rotational kinetic energy. Electrons at outer orbits have larger kinetic energies. Electrons also spin about their axes, and the energy associated with this motion is the spin energy. Other particles in the nucleus of an atom also possess spin energy. The portion of the internal energy of a system associated with the kinetic energies of the molecules is called the sensible energy (Fig. 2–20). The average velocity and the degree of activity of the molecules
are proportional to the temperature of the gas. Therefore, at higher temperatures, the molecules will possess higher kinetic energies, and as a result the system will have a higher internal energy.
The internal energy is also associated with various binding forces between the molecules of a substance, between the atoms within a molecule, and be- tween the particles within an atom and its nucleus. The forces that bind the molecules to each other are, as one would expect, strongest in solids and weakest in gases. If sufficient energy is added to the molecules of a solid or liquid, they will overcome these molecular forces and break away, turning the substance into a gas. This is a phase-change process. Because of this added energy, a system in the gas phase is at a higher internal energy level than it is in the solid or the liquid phase. The internal energy associated with the phase of a system is called the latent energy. The phase-change process can occur without a change in the chemical composition of a system. Most practical problems fall into this category, and one does not need to pay any attention to the forces binding the atoms in a molecule to each other.
An atom consists of positively charged protons and neutrons bound together by very strong nuclear forces in the nucleus, and negatively charged electrons orbiting around it. The internal energy associated with the atomic bonds in a molecule is called chemical energy. During a chemical reaction, such as a combustion process, some chemical bonds are destroyed while others are formed. As a result, the internal energy changes. The nuclear forces are much larger than the forces that bind the electrons to the nucleus. The tremendous amount of energy associated with the strong bonds within the nucleus of the atom itself is called nuclear energy (Fig. 2–21). Obviously, we need not be concerned with nuclear energy in thermodynamics unless, of course, we deal with fusion or fission reactions. A chemical reaction involves changes in the structure of the electrons of the atoms, but a nuclear reaction involves changes in the core or nucleus. Therefore, an atom preserves its identity during a chemical reaction but loses it during a nuclear reaction. Atoms may also possess electric and magnetic dipole-moment energies when subjected to external electric and magnetic fields due to the twisting of the magnetic dipoles produced by the small electric currents associated with the orbiting electrons.
The forms of energy already discussed, which constitute the total energy of a system, can be contained or stored in a system, and thus can be viewed as the static forms of energy. The forms of energy not stored in a system can be viewed as the dynamic forms of energy or as energy interactions. The dynamic forms of energy are recognized at the system boundary as they cross it, and they represent the energy gained or lost by a system during a process. The only two forms of energy interactions associated with a closed system are heat transfer and work. An energy interaction is heat transfer if its driving force is a temperature difference. Otherwise it is work, as explained later. A control volume can also exchange energy via mass transfer since any time
mass is transferred into or out of a system, the energy content of the mass is also transferred with it.
In daily life, we frequently refer to the sensible and latent forms of internal energy as heat, and we talk about heat content of bodies. In thermodynamics, however, we usually refer to those forms of energy as thermal energy to pre- vent any confusion with heat transfer.
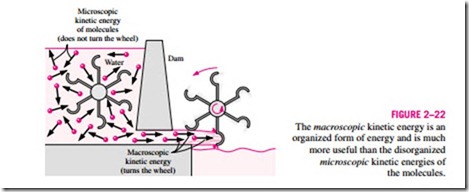
Distinction should be made between the macroscopic kinetic energy of an object as a whole and the microscopic kinetic energies of its molecules that constitute the sensible internal energy of the object (Fig. 2–22). The kinetic energy of an object is an organized form of energy associated with the orderly motion of all molecules in one direction in a straight path or around an axis. In contrast, the kinetic energies of the molecules are completely random and highly disorganized. As you will see in later chapters, the organized energy is much more valuable than the disorganized energy, and a major application area of thermodynamics is the conversion of disorganized energy (heat) into organized energy (work). You will also see that the organized energy can be converted to disorganized energy completely, but only a fraction of disorganized energy can be converted to organized energy by specially built devices called heat engines (like car engines and power plants). A similar argument can be given for the macroscopic potential energy of an object as a whole and the microscopic potential energies of the molecules.
More on Nuclear Energy
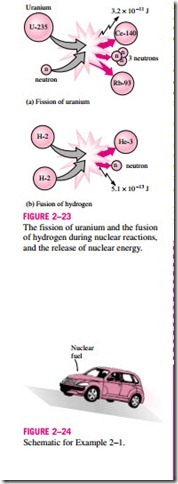
The best known fission reaction involves the split of the uranium atom (the U-235 isotope) into other elements, and is commonly used to generate electricity in nuclear power plants (429 of them in 1990, generating 311,000 MW worldwide), to power nuclear submarines and aircraft carriers, and even to power spacecraft as well as building nuclear bombs. The first nuclear chain reaction was achieved by Enrico Fermi in 1942, and the first large-scale nu- clear reactors were built in 1944 for the purpose of producing material for nu- clear weapons. When a uranium-235 atom absorbs a neutron and splits during a fission process, it produces a cesium-140 atom, a rubidium-93 atom, 3 neutrons, and 3.2 X 10-11 J of energy. In practical terms, the complete fission of 1 kg of uranium-235 releases 6.73 X 1010 kJ of heat, which is more than the heat released when 3000 tons of coal are burned. Therefore, for the same amount of fuel, a nuclear fission reaction releases several million times more energy than a chemical reaction. The safe disposal of used nuclear fuel, how- ever, remains a concern.
Nuclear energy by fusion is released when two small nuclei combine into a larger one. The huge amount of energy radiated by the sun and the other stars originates from such a fusion process that involves the combination of two hydrogen atoms into a helium atom. When two heavy hydrogen (deuterium) nuclei combine during a fusion process, they produce a helium-3 atom, a free neutron, and 5.1 X 10-13 J of energy (Fig. 2–23).
Fusion reactions are much more difficult to achieve in practice because of the strong repulsion between the positively charged nuclei, called the Coulomb repulsion. To overcome this repulsive force and to enable the two nuclei to fuse together, the energy level of the nuclei must be raised by heating them to about 100 million °C. But such high temperatures are found only in the stars or in exploding atomic bombs (the A-bomb). In fact, the uncontrolled fusion reaction in a hydrogen bomb (the H-bomb) is initiated by a small atomic bomb. The uncontrolled fusion reaction was achieved in the early 1950s, but all the efforts since then to achieve controlled fusion by massive lasers, powerful magnetic fields, and electric currents to generate power have failed.