ENERGY TRANSFER BY WORK
Work, like heat, is an energy interaction between a system and its surroundings. As mentioned earlier, energy can cross the boundary of a closed system in the form of heat or work. Therefore, if the energy crossing the boundary of a closed system is not heat, it must be work. Heat is easy to recognize: Its driving force is a temperature difference between the system and its surroundings. Then we can simply say that an energy interaction that is not caused by a temperature difference between a system and its surroundings is work. More specifically, work is the energy transfer associated with a force acting through a distance. A rising piston, a rotating shaft, and an electric wire crossing the system boundaries are all associated with work interactions.
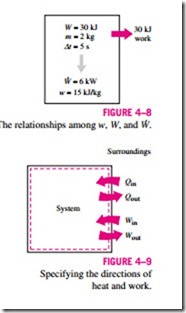
Work is also a form of energy transferred like heat and, therefore, has energy units such as kJ. The work done during a process between states 1 and 2 is denoted by W12, or simply W. The work done per unit mass of a system is denoted by w and is expressed as
The work done per unit time is called power and is denoted W (Fig. 4–8). The unit of power is kJ/s, or kW.
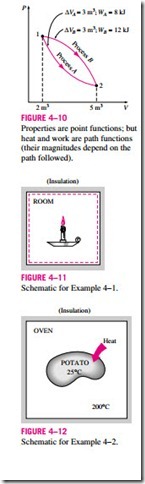
Heat and work are directional quantities, and thus the complete description of a heat or work interaction requires the specification of both the magnitude and direction. One way of doing that is to adopt a sign convention. The gen- erally accepted formal sign convention for heat and work interactions is as follows: heat transfer to a system and work done by a system are positive; heat transfer from a system and work done on a system are negative. Another way is to use the subscripts in and out to indicate direction (Fig. 4–9). For example, a work input of 5 kJ can be expressed as Win = 5 kJ, while a heat loss of 3 kJ can be expressed as Qout = 3 kJ. When the direction of a heat or work interaction is not known, we can simply assume a direction for the interaction (using the subscript in or out) and solve for it. A positive result indicates the assumed direction is right. A negative result, on the other hand, indicates that the direction of the interaction is the opposite of the assumed direction. This is just like assuming a direction for an unknown force when solving a statics problem, and reversing the direction when a negative result is obtained for the The relationships among w, W, and W.
force. We will use this intuitive approach in this book as it eliminates the need to adopt a formal sign convention and the need to carefully assign negative values to some interactions.
Note that a quantity that is transferred to or from a system during an inter- action is not a property since the amount of such a quantity depends on more than just the state of the system. Heat and work are energy transfer mecha- nisms between a system and its surroundings, and there are many similarities between them:
1. Both are recognized at the boundaries of a system as they cross the boundaries. That is, both heat and work are boundary phenomena.
2. Systems possess energy, but not heat or work.
3. Both are associated with a process, not a state. Unlike properties, heat or work has no meaning at a state.
4. Both are path functions (i.e., their magnitudes depend on the path followed during a process as well as the end states).
Path functions have inexact differentials designated by the symbol d. There- fore, a differential amount of heat or work is represented by dQ or dW, respectively, instead of dQ or dW. Properties, however, are point functions (i.e., they depend on the state only, and not on how a system reaches that state), and they have exact differentials designated by the symbol d. A small change in volume, for example, is represented by dV, and the total volume change during a process between states 1 and 2 is
That is, the volume change during process 1–2 is always the volume at state 2 minus the volume at state 1, regardless of the path followed (Fig. 4–10). The total work done during process 1–2, however, is
That is, the total work is obtained by following the process path and adding the differential amounts of work (dW) done along the way. The integral of dW is not W2 – W1 (i.e., the work at state 2 minus work at state 1), which is meaningless since work is not a property and systems do not possess work at a state.
Electrical Work
It was pointed out in Example 4–3 that electrons crossing the system boundary do electrical work on the system. In an electric field, electrons in a wire move under the effect of electromotive forces, doing work. When N coulombs of electrical charge move through a potential difference V, the electrical work done is
Incoming search terms:
- energy transfer in the form mass heat work
- when is the energy crossing the boundaries of a closed system heat and when is it work ?
- when is the energy crossing the boundaries of closed system and when is it work