ACCURACY, PRECISION, AND SIGNIFICANT DIGITS
In engineering calculations, the supplied information is not known to more than a certain number of significant digits, usually three digits. Consequently, the results obtained cannot possibly be accurate to more significant digits. Reporting results in more significant digits implies greater accuracy than exists, and it should be avoided.
Regardless of the system of units employed, engineers must be aware of three principles that govern the proper use of numbers: accuracy, precision, and significant digits. For engineering measurements, they are defined as follows:
• Accuracy error (inaccuracy) is the value of one reading minus the true value. In general, accuracy of a set of measurements refers to the closeness of the average reading to the true value. Accuracy is generally associated with repeatable, fixed errors.
• Precision error is the value of one reading minus the average of readings.
In general, precision of a set of measurements refers to the fineness of the resolution and the repeatability of the instrument. Precision is generally associated with unrepeatable, random errors.
Clearly, anemometer A is more precise, since none of the readings differs by more than 0.1 m/s from the average. However, the average is 25.58 m/s, 0.58 + m/s greater than the true wind speed; this indicates significant bias error, also + called constant error. On the other hand, anemometer B is not very precise, + + since its readings swing wildly from the average; but its overall average is + +
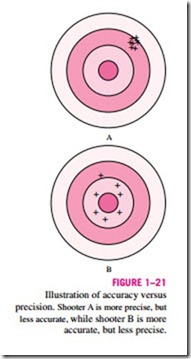
much closer to the true value. Hence, anemometer B is more accurate than anemometer A, at least for this set of readings, even though it is less precise. The difference between accuracy and precision can be illustrated effectively by analogy to shooting a gun at a target, as sketched in Fig. 1–21. Shooter A is very precise, but not very accurate, while shooter B has better overall accu- racy, but less precision.
Many engineers do not pay proper attention to the number of significant digits in their calculations. The least significant numeral in a number implies the precision of the measurement or calculation. For example, a result written as 1.23 (three significant digits) implies that the result is precise to within one
digit in the second decimal place, i.e., the number is somewhere between
1.22 and 1.24. Expressing this number with any more digits would be mis- leading. The number of significant digits is most easily evaluated when the number is written in exponential notation; the number of significant digits can then simply be counted, including zeroes. Some examples are shown in Table 1–3.
When performing calculations or manipulations of several parameters, the final result is generally only as precise as the least precise parameter in the problem. For example, suppose A and B are multiplied to obtain C. If A = 2.3601 (five significant digits), and B = 0.34 (two significant digits), then C = 0.80 (only two digits are significant in the final result). Note that most stu- dents are tempted to write C = 0.802434, with six significant digits, since that is what is displayed on a calculator after multiplying these two numbers.
Let’s analyze this simple example carefully. Suppose the exact value of B is 0.33501, which is read by the instrument as 0.34. Also suppose A is exactly 2.3601, as measured by a more accurate instrument. In this case, C = A X B = 0.79066 to five significant digits. Note that our first answer, C = 0.80 is off by one digit in the second decimal place. Likewise, if B is 0.34499, and is read by the instrument as 0.34, the product of A and B would be 0.81421 to five significant digits. Our original answer of 0.80 is again off by one digit in the second decimal place. The main point here is that 0.80 (to two significant dig- its) is the best one can expect from this multiplication since, to begin with, one of the values had only two significant digits. Another way of looking at this is to say that beyond the first two digits in the answer, the rest of the digits are meaningless or not significant. For example, if one reports what the calculator displays, 2.3601 times 0.34 equals 0.802434, the last four digits are meaning- less. As shown, the final result may lie between 0.79 and 0.81—any digits be- yond the two significant digits are not only meaningless, but misleading, since they imply to the reader more precision than is really there.
As another example, consider a 3.75-L container filled with gasoline whose density is 0.845 kg/L, and determine its mass. Probably the first thought that comes to your mind is to multiply the volume and density to obtain 3.16875 kg for the mass, which falsely implies that the mass so determined is precise to six significant digits. In reality, however, the mass cannot be more precise than three significant digits since both the volume and the density are precise to three significant digits only. Therefore, the result should be rounded to three significant digits, and the mass should be reported to be 3.17 kg in-
stead of what the calculator displays. The result 3.16875 kg would be correct only if the volume and density were given to be 3.75000 L and 0.845000 kg/L, respectively. The value 3.75 L implies that we are fairly confident that the vol- ume is precise within ±0.01 L, and it cannot be 3.74 or 3.76 L. However, the volume can be 3.746, 3.750, 3.753, etc., since they all round to 3.75 L (Fig. 1–22).
You should also be aware that sometimes we knowingly introduce small errors in order to avoid the trouble of searching for more accurate data. For ex- ample, when dealing with liquid water, we just use the value of 1000 kg/m3
for density, which is the density value of pure water at 0ºC. Using this value at 75ºC will result in an error of 2.5 percent since the density at this tempera- ture is 975 kg/m3. The minerals and impurities in the water will introduce ad- ditional error. This being the case, you should have no reservation in rounding the final results to a reasonable number of significant digits. Besides, having a few percent uncertainty in the results of engineering analysis is usually the norm, not the exception.
When writing intermediate results in a computation, it is advisable to keep several “extra” digits to avoid round-off errors; however, the final result should be written with the number of significant digits taken into consideration. The reader must also keep in mind that a certain number of significant digits of precision in the result does not necessarily imply the same number of digits of overall accuracy. Bias error in one of the readings may, for example, significantly reduce the overall accuracy of the result, perhaps even rendering the last significant digit meaningless, and reducing the overall number of reliable digits by one. Experimentally determined values are subject to measurement errors, and such errors will reflect in the results obtained. For example, if the density of a substance has an uncertainty of 2 percent, then the mass determined using this density value will also have an uncertainty of 2 percent. Finally, when the number of significant digits is unknown, the accepted en- gineering standard is three significant digits. Therefore, if the length of a pipe is given to be 40 m, we will assume it to be 40.0 m in order to justify using three significant digits in the final results.