THE CARNOT REFRIGERATOR AND HEAT PUMP
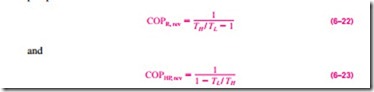
A refrigerator or a heat pump that operates on the reversed Carnot cycle is called a Carnot refrigerator, or a Carnot heat pump. The coefficient of performance of any refrigerator or heat pump, reversible or irreversible, is given by Eqs. 6–11 and 6–13 as
where QL is the amount of heat absorbed from the low-temperature medium and QH is the amount of heat rejected to the high-temperature medium. The COPs of all reversible refrigerators or heat pumps can be determined by replacing the heat transfer ratios in the above relations by the ratios of the absolute temperatures of the high- and low-temperature reservoirs, as expressed by Eq. 6–18. Then the COP relations for reversible refrigerators and heat pumps become
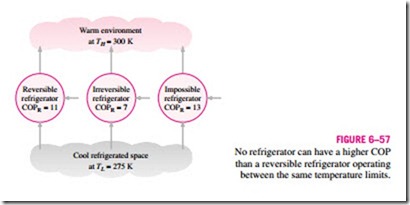
These are the highest coefficients of performance that a refrigerator or a heat pump operating between the temperature limits of TL and TH can have. All actual refrigerators or heat pumps operating between these temperature limits (TL and TH) will have lower coefficients of performance (Fig. 6–57).
The coefficients of performance of actual and reversible refrigerators operating between the same temperature limits can be compared as follows:
A similar relation can be obtained for heat pumps by replacing all COPR’s in Eq. 6–24 by COPHP.
The COP of a reversible refrigerator or heat pump is the maximum theoretical value for the specified temperature limits. Actual refrigerators or heat pumps may approach these values as their designs are improved, but they can never reach them.
As a final note, the COPs of both the refrigerators and the heat pumps de- crease as TL decreases. That is, it requires more work to absorb heat from lower-temperature media. As the temperature of the refrigerated space ap- proaches zero, the amount of work required to produce a finite amount of refrigeration approaches infinity and COPR approaches zero.
