FORCES IN LIQUIDS
The study of liquids is divided into two main parts: liquids at rest, hydrostatics; and liquids in motion, hydraulics. The effect of liquids at rest can often be expressed by simple formulas. The effects of liquids in motion are more difficult to express because of frictional and other factors whose actions cannot be expressed by simple mathematics.
Liquids are almost incompressible. For example, if a pressure of 100 pounds per square inch, psi, is applied to a given volume of water that is at atmospheric pressure, the volume will decrease by only 0.03 percent. It would take a force of approximately 32 tons to reduce its volume by 10 percent; however, when this force is removed, the water immediately returns to its original volume. Other liquids behave in about the same manner as water.
Another characteristic of a liquid is the tendency to keep its free surface level. If the surface is not level, liquids will flow in the direction that will tend to make the surface level.
LIQUIDS AT REST (HYDROSTATICS)
In the study of fluids at rest, we are concerned with the transmission of force and the factors that affect the forces in liquids. Additionally, pressure in and on liquids and factors affecting pressure are of great importance.
PRESSURE AND FORCE
The terms force and pressure are used extensively in the study of fluid power. It is essential that we distinguish between these terms. Force is the total pressure applied to or generated by a system. It is the total pressure exerted against the total area of a particular surface and is expressed in pounds or grams.
Pressure is the amount of force applied to each unit area of a surface and is expressed in pounds per square inch, lb/in2 (psi) or grams per square centimeter, grn/cm2• Pres sure may be exerted in one direction, in several directions, or in all directions.
A formula is used in computing force, pressure, and area in fluid power systems. In this formula, P refers to pressure, F indicates force, and A represents area. Force equals pressure times area. Thus, the formula is written
ATMOSPHERIC PRESSURE
The atmosphere is the entire mass of air that surrounds the earth. Although it extends upward for about 500 miles, the section of primary interest is the portion that rests on the earth’s surface and extends upward for about 7 1/2 miles. This layer is called the troposphere.
If a column of air I inch square extended to the “top” of the atmosphere could be weighed, this column of air would weigh approximately 14.7 pounds at sea level. Thus, atmospheric pressure, at sea level, is approximately 14.7 pounds per square inch or psi.
Atmospheric pressure decreases by approximately 1.0 psi for every 2,343 feet of elevation. At elevations below sea level, such as in excavations and depressions, atmospheric pressure increases. Pressures under water differ from those under air only because the weight of the water must be added to the pressure of the air.
Atmospheric pressure can be measured by any of several methods. The common laboratory method uses a mercury column barometer. The height of the mercury column serves as an indicator of atmospheric pressure. At sea level and at a temperature of Oo Celsius (T), the height of the mercury column is approximately 30 inches, or 76 cen timeters. This represents a pressure of approximately 14.7 psia. The 30-inch column is used as a reference standard.
Atmospheric pressure does not vary uniformly with altitude. It changes more rapidly at lower altitudes because of the compressibility of air, which causes the air layers close to the earth’s surface to be compressed by the air masses above them. This effect, however, is partially counteracted by the contraction of the upper layers due to cooling. The cooling tends to increase the density of the air.
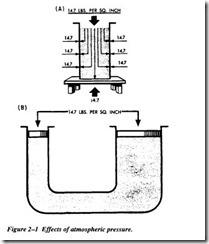
Atmospheric pressures are quite large, but in most instances practically the same pressure is present on all sides of objects so that no single surface is subjected to a greater load. Atmospheric pressure acting on the surface of a liquid (Figure 2-lA) is transmitted equally throughout the liquid to the walls of the container, but is balanced by the same atmospheric pressure acting on the outer walls of the container. Inpart B of Figure 2-1, atmospheric pressure acting on the surface of one piston is balanced by the same pres sure acting on the surface of the other piston. The different areas of the two surfaces make no difference, since for a unit of area, pressures are balanced.
PASCAL’S LAW
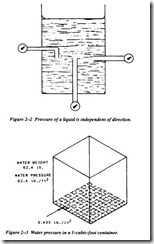
The foundation of modern hydraulics was established when Pascal discovered that pressure in a fluid acts equally in all directions. This pressure acts at right angles to the containing surfaces. If some type of pressure gauge, with an exposed face, is placed beneath the surface of a liquid (Figure 2-2) at a specific depth and pointed in different directions, the pressure will read the same. Thus, we can say that pressure in a liquid is independent of direction.
Pressure due to weight of a liquid, at any level, depends on the depth of the fluid from the surface. If the exposed face of the pressure gauge in Figure 2-2 is moved closer to the surface of the liquid, the indicated pressure will be less.
When the depth is doubled, the indicated pressure is also doubled. Thus, the pressure in a liquid is directly proportional to the depth. Consider a container with vertical sides (Figure 2-3) that are 1 foot high and 1 foot wide.
Let it be filled with water 1 foot deep, thus providing 1 cubic foot of water. We learned earlier in this chapter that 1 cubic foot of water weighs 62.4 pounds. Using
this information and the equation for pressure we can calculate the pressure on the bottom of the container.
Since there are 144 square inches in 1 square foot, this can be stated as follows: The weight of a column of water 1 foot high, having a cross-sectional area of 1 square inch, is 0.433 pounds. If the depth of the column is tripled, the weight of the column will be 3 x 0.433 or 1.299 pounds and the pressure at the bottom will be 1.299 lb/in2(psi), since the pressure is equal to the force divided by the area. Thus, the pressure at any depth in a liquid is equal to the weight of the column of liquid at the depth divided by the cross-sectional area of the column at that depth. The volume of a liquid that produces the pressure is referred to as the fluid head of the liquid. The pressure of a liquid due to its fluid head is also dependent on the density of the liquid.
If we let A equal any cross-sectional area of a liquid column and h equal the depth of the column, the volume becomes Ah. Using the equation D = w;v, the weight of the liquid above area A is equal to AhD, or
Since pressure is equal to the force per unit area, set A equal to 1. Then the formula for pressure becomes
It is essential that h and D be expressed in similar units. That is, if D is expressed in pounds per cubic foot, the value of h must be expressed in feet. If the desired pressure is to be expressed in pounds per square inch, the pressure formula becomes
Pascal was also the first to prove by experiment that the shape and volume of a container in no way alters pressure. Thus, in Figure 2-4, if the pressure due to the weight of the liquid at a point on horizontal line H is 8 psi, the pressure is 8 psi everywhere at level H in the system.