Power requirements
Information on the power required for a pneumatic conveying system is just as import- ant for its successful operation as design data for the selection of the correct pipeline bore and conveying line pressure drop for a given system. In cases where alternative combinations of parameters can be selected, an economic assessment of the best system will be well worthwhile carrying out, as mentioned earlier.
With so many cases to consider, and a wide range of air movers available (see Chapter 6), it is almost an impossible task to determine power requirements accurately. Quite clearly some air movers will be more efficient than others, and a smooth transition is unlikely to be made from one type of air mover into that for the next available. In order to overcome these problems, and to provide data that is both realistic and comparable, a simple mathematical model has been used to evaluate the compression work.
The model is based on the isothermal compression of air and for this, data is required on air flow rate (mass or volumetric), together with conveying line pressure drop values. This, of course, is the ideal case and does not take account of thermo- dynamic irreversibility or transmission losses. To allow for these the basic model is multiplied by a constant. A value of two has been used for this constant, and this has been found to provide reasonable agreement with manufacturers’ literature for a wide range of air movers, air flow rates and delivery pressures (see Equations (6.5) and (6.6)). The main advantage of using such a model is that it provides a degree of uniformity when making comparisons between variables.
In this introductory chapter only a passing mention is made of power requirements as this is considered in more detail in Chapter 11. In order to supplement the earlier work presented here, and to illustrate the order of magnitude of the power require- ments for pneumatic conveying, the influence of material type, conveying distance and pipeline bore are considered briefly here.
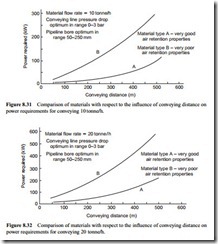
Influence of conveying distance
The influence of conveying distance on material flow rate is illustrated specifically in Figures 8.7 and 8.8, where it was shown that for a given pipeline bore and conveying line pressure drop there was a marked fall in material flow rate with increase in con- veying distance. On this basis the power required to convey a material with very poor air retention properties will be approximately constant, since the conveying line inlet air velocity remains constant. For a material with very good air retention properties, however, there will have to be an increase in power with increase in conveying distance. This is due to the fact that as conveying distance increases, solids loading ratio decreases, and so conveying line inlet air velocity and hence air flow rate have to be increased.
The basis of comparison presented in Figures 8.31 and 8.32 is for conveying at a given flow rate over a range of distances. In Figure 8.31 a material flow rate of 10 tonne/h is considered and in Figure 8.32 it is 20 tonne/h. These are both plots of power required against conveying distance, and the two extremes of material type are represented on each. In order to achieve a constant material flow rate with respect to conveying distance, changes in both pipeline bore and conveying line pressure drop need to be made. The combination of parameters, within the ranges considered, have been selected that result in the lowest value of power required.
This provides possibly the best means by which materials can be compared. The change in relative spacing, with respect to conveying distance, between the two curves on each figure is due to the change in air requirements for materials with good air retention properties, as discussed above. The difference in power requirements for the two materials is approximately in the ratio of 3:1 over a distance of about 500 m. This is as close as they will get, for over this distance both materials have to be conveyed in suspension flow. For shorter distances the difference is of the order of 6:1, for the comparison is between suspension and non-suspension flow.
Part of this difference can be attributed to the difference in conveying characteristics between the two materials. When conveyed under identical conveying conditions the difference is of the order of 2:1, as shown earlier with Figure 8.2. Any differences beyond this value can be attributed to the different velocity levels at which the mater- ials are conveyed. The largest differences, therefore, occur with shorter conveying distances, where materials with very good air retention properties can be conveyed in dense phase and hence at low velocity.
System considerations
It is clear from this that if a material with very poor air retention properties could be conveyed in dense phase and at low velocity in an alternative pneumatic conveying
system, such as a pulse phase or plug control system, it is possible that energy savings could be made over conventional conveying systems. The operating characteristics of such a system is presented in Figure 8.2 and so this throws some doubt on the possi- bility. Although the material will be conveyed at a lower velocity, the material flow rate reduces with decrease in velocity so that a larger bore pipeline would be needed to convey the material. This means that more air will be required, and hence more power, and so it is likely that the energy saving will be marginal.
Influence of pipeline bore
The influence of pipeline bore on material flow rate is illustrated specifically in Figures 8.11 and 8.12, where it was shown that for a given conveying distance and conveying line pressure drop there was a marked increase in material flow rate with increase in pipeline bore. The basis for comparison presented in Figures 8.33 and 8.34 is for conveying at a given flow rate with a range of pipeline bores.
In Figure 8.33 a material flow rate of 10 tonne/h is considered, conveyed over a distance of 200 m, and in Figure 8.34 the material flow rate is 20 tonne/h and the distance is 100 m. These are both plots of power required against pipeline bore, and the two extremes of material type are represented on each. In order to achieve a constant material flow rate with respect to pipeline bore an appropriate value of conveying line pressure drop was selected.
Once again this probably provides the best means by which materials can be com- pared. These particular curves also show very interesting, and different, trends for both materials considered.
Materials with good air retention properties
With respect to materials having good air retention properties it is clear that for minimum power requirements, small bore pipelines and high air supply pressures should
be used. This is particularly the case for short distance conveying. In Figure 8.34, for example, with the material conveyed over 100 m, the power requirement for a 250 mm bore pipeline is about six times that for a 50 mm bore pipeline for the identical duty.
The reason for this is that in a small bore pipeline very little air is needed, although it is obviously required at a high pressure. This means that for a given material flow rate the solids loading ratio in a small bore pipeline will be very high, which in turn means that a low conveying line inlet air velocity can be employed. In a large bore pipeline a large quantity of air will be required, although at very low pressure.
This means that for a given material flow rate the solids loading ratio in a large bore pipeline will be very low, which means that a high conveying line inlet air velocity will have to be used. The combination of air flow rate and pressure required is far greater for the larger bore, dilute phase conveying case, and so for any material capable of being conveyed in dense phase, operating costs will be much lower in small bore pipelines using high pressure air.
This analysis is based on continuously operating systems. For systems employing air pressures of 3 bar and above, blow tanks are likely to be used. These are often batch conveying systems and in this case the relationship between the steady state flow rate achieved during batch conveying and the time averaged mean will have to be taken into account, as considered in Section 4.4.2.2. With high pressure systems it would be recommended that the pipeline should be stepped to a larger bore part way along its length and the potential influence of this is considered in Chapter 14.
Materials with poor air retention properties
In the case of materials having very poor air retention properties exactly the reverse situation applies. For these materials large bore pipelines and low air pressures should be used for minimum power requirements. In the cases presented in Figures 8.33 and 8.34 almost 50 per cent more power is required to convey the material in a small bore pipeline.
The reason for the poor performance of small bore pipelines is that high air supply pressures are required. In single bore pipelines very high mean conveying air velocities will result. High velocities, particularly in small bore pipelines result in high pressure drops, both for the empty line for the air only, and for the conveying of the material.
In large bore pipelines much lower conveying line pressure drops will be required to convey the material and so the mean conveying air velocity will be much lower. The air only pressure drop in a large bore pipeline is also lower than that for a small bore pipeline, even for the same value of conveying air velocity.
For the small bore pipeline an improvement in performance is possible. This is because a high air pressure is required and so a stepped pipeline could be employed. This would help to reduce the very high velocities that result and so improve the performance. This point is also considered further in Chapter 14.
Material compatibility
Material compatibility was considered earlier in relation to conveying air requirements at Section 8.3.1.2. Figures 8.33 and 8.34, however, show another aspect of this problem, for if such dissimilar materials have to be conveyed in a common pipeline, a bore selected for one material may not be suitable for another material. The difference in power requirements can also be very great, particularly with small bore pipelines. This problem can often be solved by using stepped pipelines and this is explored in Chapter 19.