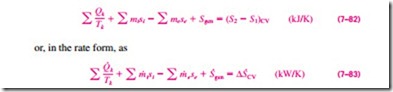■ ENTROPY BALANCE
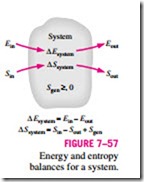
The property entropy is a measure of molecular disorder or randomness of a system, and the second law of thermodynamics states that entropy can be created but it cannot be destroyed. Therefore, the entropy change of a system during a process is greater than the entropy transfer by an amount equal to the entropy generated during the process within the system, and the increase of entropy principle for any system is expressed as (Fig. 7–57)
which is a verbal statement of Eq. 7–9. This relation is often referred to as the entropy balance and is applicable to any system undergoing any process. The entropy balance relation above can be stated as: the entropy change of a system during a process is equal to the net entropy transfer through the system boundary and the entropy generated within the system. Next we discuss the various terms in that relation.
Entropy Change of a System
Despite the reputation of entropy as being vague and abstract and the intimidation associated with it, entropy balance is actually easier to deal with than energy balance since, unlike energy, entropy does not exist in various forms. Therefore, the determination of entropy change of a system during a process involves evaluating entropy of the system at the beginning and at the end of the process and taking their difference. That is,
Note that entropy is a property, and the value of a property does not change unless the state of the system changes. Therefore, the entropy change of a system is zero if the state of the system does not change during the process. For example, the entropy change of steady-flow devices such as nozzles, compressors, turbines, pumps, and heat exchangers is zero during steady operation.
When the properties of the system are not uniform, the entropy of the sys- tem can be determined by integration from
where V is the volume of the system and r is density.
Mechanisms of Entropy Transfer, Sin and Sout
Entropy can be transferred to or from a system by two mechanisms: heat
transfer and mass flow (in contrast, energy is transferred by work also). Entropy transfer is recognized at the system boundary as it crosses the bound- ary, and it represents the entropy gained or lost by a system during a process. The only form of entropy interaction associated with a fixed mass or closed system is heat transfer, and thus the entropy transfer for an adiabatic closed system is zero.
1 Heat Transfer
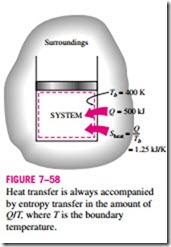
Heat is, in essence, a form of disorganized energy, and some disorganization (entropy) will flow with heat. Heat transfer to a system increases the entropy of that system and thus the level of molecular disorder or randomness, and heat transfer from a system decreases it. In fact, heat rejection is the only way the entropy of a fixed mass can be decreased. The ratio of the heat transfer Q at a location to the absolute temperature T at that location is called the entropy flow or entropy transfer and is expressed as (Fig. 7–58)
by entropy transfer in the amount of Q/T, where T is the boundary temperature.
The quantity Q/T represents the entropy transfer accompanied by heat transfer, and the direction of entropy transfer is the same as the direction of heat transfer since absolute temperature T is always a positive quantity.
When the temperature T is not constant, the entropy transfer during a process 1-2 can be determined by integration (or by summation if appropri- ate) as
where Qk is the heat transfer through the boundary at temperature Tk at location k.
When two systems are in contact, the entropy transfer from the warmer sys- tem is equal to the entropy transfer into the cooler one at the point of contact. That is, no entropy can be created or destroyed at the boundary since the boundary has no thickness and occupies no volume.
Note that work is entropy-free, and no entropy is transferred by work. Energy is transferred by both heat and work, whereas entropy is transferred only by heat. That is,
The first law of thermodynamics makes no distinction between heat transfer and work; it considers them as equals. The distinction between heat trans- fer and work is brought out by the second law: an energy interaction that is accompanied by entropy transfer is heat transfer, and an energy interaction that is not accompanied by entropy transfer is work. That is, no entropy is ex- changed during a work interaction between a system and its surroundings. Thus, only energy is exchanged during work interaction whereas both energy and entropy are exchanged during heat transfer (Fig. 7–59).
2 Mass Flow
Mass contains entropy as well as energy, and the entropy and energy contents of a system are proportional to the mass. (When the mass of a system is doubled, so are the entropy and energy contents of the system.) Both entropy and energy are carried into or out of a system by streams of matter, and the rates of entropy and energy transport into or out of a system are proportional to the mass flow rate. Closed systems do not involve any mass flow and thus any en- tropy transfer by mass. When a mass in the amount of m enters or leaves a sys- tem, entropy in the amount of ms, where s is the specific entropy (entropy per unit mass entering or leaving), accompanies it (Fig. 7–60). That is,
Therefore, the entropy of a system increases by ms when mass in the amount of m enters and decreases by the same amount when the same amount of mass at the same state leaves the system. When the properties of the mass change during the process, the entropy transfer by mass flow can be determined by integration from
where Ac is the cross-sectional area of the flow and ‘V is the local velocity normal to dAc.
Entropy Generation
Irreversibilities such as friction, mixing, chemical reactions, heat transfer through a finite temperature difference, unrestrained expansion, nonquasiequilibrium compression, or expansion always cause the entropy of a system to increase, and entropy generation is a measure of the entropy created by such effects during a process.
For a reversible process (a process that involves no irreversibilities), the entropy generation is zero and thus the entropy change of a system is equal to the entropy transfer. Therefore, the entropy balance relation in the reversible case becomes analogous to the energy balance relation, which states that energy change of a system during a process is equal to the energy transfer during that process. However, note that the energy change of a system equals the energy transfer for any process, but the entropy change of a system equals the entropy transfer only for a reversible process.
The entropy transfer by heat Q/T is zero for adiabatic systems, and the entropy transfer by mass ms is zero for systems that involve no mass flow across their boundary (i.e., closed systems).
Entropy balance for any system undergoing any process can be expressed more explicitly as
where all the quantities are expressed per unit mass of the system. Note that for a reversible process, the entropy generation term Sgen drops out from all of the relations above.
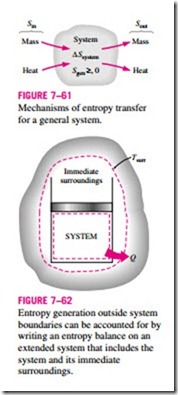
The term Sgen represents the entropy generation within the system boundary only (Fig. 7–61), and not the entropy generation that may occur outside the system boundary during the process as a result of external irreversibilities. Therefore, a process for which Sgen = 0 is internally reversible, but not necessarily totally reversible. The total entropy generated during a process can be determined by applying the entropy balance to an extended system that includes the system itself and its immediate surroundings where external irreversibilities might be occurring (Fig. 7–62). Also, the entropy change in this case is equal to the sum of the entropy change of the system and the entropy change of the immediate surroundings. Note that under steady conditions, the state and thus the entropy of the immediate surroundings (let us call it the “buffer zone”) at any point will not change during the process, and the entropy change of the buffer zone will be zero. The entropy change of the buffer zone, if any, is usually small relative to the entropy change of the system, and thus it is usually disregarded.
When evaluating the entropy transfer between an extended system and the surroundings, the boundary temperature of the extended system is simply taken to be the environment temperature.
Closed Systems
A closed system involves no mass flow across its boundaries, and its entropy change is simply the difference between the initial and final entropies of the system. The entropy change of a closed system is due to the entropy transfer accompanying heat transfer and the entropy generation within the system boundaries. Taking the positive direction of heat transfer to be to the system, the general entropy balance relation (Eq. 7–76) can be expressed for a closed system as
The entropy balance relation above can be stated as: the entropy change of a closed system during a process is equal to the sum of the net entropy transferred through the system boundary by heat transfer and the entropy generated within the system boundaries.
For an adiabatic process (Q = 0), the entropy transfer term in the above relation drops out and the entropy change of the closed system becomes equal to the entropy generation within the system boundaries. That is,
Noting that any closed system and its surroundings can be treated as an adiabatic system and the total entropy change of a system is equal to the sum of the entropy changes of its parts, the entropy balance for a closed system and its surroundings can be written as
where DSsystem = m(s2 – s1) and the entropy change of the surroundings can be determined from DSsurr = Qsurr / Tsurr if its temperature is constant. At initial stages of studying entropy and entropy transfer, it is more instructive to start with the general form of the entropy balance (Eq. 7–76) and to simplify it for the problem under consideration. The specific relations above are convenient to use after a certain degree of intuitive understanding of the material is achieved.
Control Volumes
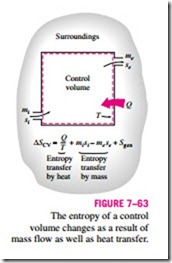
The entropy balance relations for control volumes differ from those for closed systems in that they involve one more mechanism of entropy exchange: mass Entropy transfer by heat Entropy transfer by mass flow across the boundaries. As mentioned earlier, mass possesses entropy as well as energy, and the amounts of these two extensive properties are proportional to the amount of mass (Fig. 7–63).
Taking the positive direction of heat transfer to be to the system, the general entropy balance relations (Eqs. 7–76 and 7–77) can be expressed for control volumes as
This entropy balance relation can be stated as: the rate of entropy change within the control volume during a process is equal to the sum of the rate of entropy transfer through the control volume boundary by heat transfer, the net rate of entropy transfer into the control volume by mass flow, and the rate of entropy generation within the boundaries of the control volume as a result of irreversibilities.
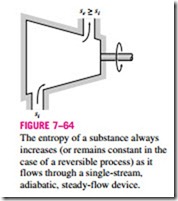
Most control volumes encountered in practice such as turbines, compressors, nozzles, diffusers, heat exchangers, pipes, and ducts operate steadily, and thus they experience no change in their entropy. Therefore, the entropy balance relation for a general steady-flow process can be obtained from Eq. 7–83 by setting D · = 0 and rearranging to give
which indicates that the specific entropy of the fluid must increase as it flows through an adiabatic device since · > 0 (Fig. 7–64). If the flow through the device is reversible and adiabatic, then the entropy will remain constant, se = si, regardless of the changes in other properties.
Entropy Generation Associated with a Heat Transfer Process
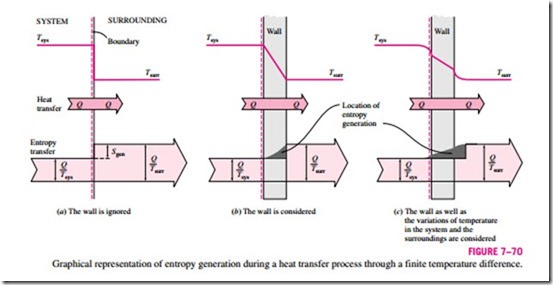
In Example 7–21 it is determined that 0.4 kJ/K of entropy is generated during the heat transfer process, but it is not clear where exactly the entropy generation takes place, and how. To pinpoint the location of entropy generation, we need to be more precise about the description of the system, its surroundings, and the system boundary.
In that example, we assumed both the system and the surrounding air to be isothermal at 100°C and 25°C, respectively. This assumption is reasonable if both fluids are well mixed. The inner surface of the wall must also be at 100°C while the outer surface is at 25°C since two bodies in physical contact must have the same temperature at the point of contact. Considering that entropy transfer with heat transfer Q through a surface at constant temperature T is Q/T, the entropy transfer from the water into the wall is Q/Tsys = 1.61 kJ/K. Likewise, entropy transfer from the outer surface of the wall into the surrounding air is Q/Tsurr = 2.01 kJ/K. Obviously, entropy in the amount of
2.01 – 1.61 = 0.4 kJ/K is generated in the wall, as illustrated in Fig. 7–70b. Identifying the location of entropy generation enables us to determine whether a process is internally reversible. A process is internally reversible if no entropy is generated within the system boundaries. Therefore, the heat transfer process discussed in Example 7–21 is internally reversible if the inner surface of the wall is taken as the system boundary, and thus the system excludes the container wall. If the system boundary is taken to be the outer surface of the container wall, then the process is no longer internally reversible since the wall, which is the site of entropy generation, is now part of the system.
For thin walls, it is very tempting to ignore the mass of the wall and to re- gard the wall as the boundary between the system and the surroundings. This seemingly harmless choice hides the site of the entropy generation from view and is a source of confusion. The temperature in this case drops suddenly from Tsys to Tsurr at the boundary surface, and confusion arises as to which temperature to use in the relation Q/T for entropy transfer at the boundary.
Note that if the system and the surrounding air are not isothermal as a result of insufficient mixing, then part of the entropy generation will occur in both the system and the surrounding air in the vicinity of the wall, as shown in Fig. 7–70c.