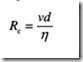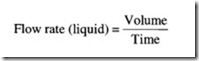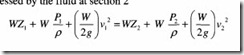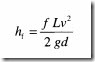Flow
Pascal’s law holds good only for liquids, which are at rest or in the static state. As stated earlier, the study of this science dealing with liquids at rest is referred to as Hydrostatics. The study of liquids in motion can be discussed under two headings, Hydrokinetics and Hydrodynamics.
Hydrokinetics deals with the motion of fluid particles without considering the forces causing the motion. The velocity at any point in the flow field at any time is studied in this branch of fluid mechanics. Once this velocity is known, the pressure distribution and the forces acting on the fluid can be determined. Hydrodynamics is the study of fluid motion that includes the forces causing the flow.
Fluid motion can be described by two methods. They are:
1. Lagrangian method
2. Eulerian method.
In the Lagrangian method a single fluid particle is followed during its motion and its characteristics such as pressure, density, velocity, acceleration, etc. are described.
In the Eulerian method, any point in the space occupied by the fluid is selected and an observation is made on the changes in parameters such as pressure, density, velocity, and acceleration at this point. The Eulerian method is generally followed and is most preferred, when it comes to analyzing hydraulic systems.
No study of flow is complete without understanding three important principles related to the phenomenon of flow, which are as follows.
1. Flow makes it go: The actuator must be supplied with flow for anything in a hydraulic system to move. The cylinder is normally retracted and requires flow to extend itself. The extension and retraction functions are accomplished with the help of a direction control valve.
2. Rate of flow determines speed: The rate of flow usually measured in gallons per minute or gpm is determined by the pump. The speed of the actuator changes with variation in pump outlet flow.
3. Changes in actuator volume displacement will change actuator speed at a given flow rate: When the cylinder retracts, less volume needs to be displaced because of the space occupied by the cylinder rod. This results in a faster actuator cycle. Therefore, there is always a difference in actuator speed between the extend and retract functions.
Meaning of flow
Flow velocity is very important in the design of a hydraulic system. When we speak of fluid flow down a pipe in a hydraulic system, the term flow in itself conveys three distinct meanings, which are:
1. Volumetricflow, which is a measure of the volume of a fluid passing through a point in unit time.
2. Mass flow, which is a measure of the mass of a fluid passing through a point in unit time.
3. Velocity of flow, which is a measure of the linear speed of a fluid passing through the point of measurement.
Types of fluid flow
Fluid flow can be classified as follows:
• Steady and unsteady flows
• Uniform and non-uniform flows
• Laminar and turbulent flows
• Rotational and non-rotational flows.
Steady flow
Fluid flow is said to be steady if at any point in the flowing fluid, important characteristics such as pressure, density, velocity, temperature, etc. that are used to describe the behavior of a fluid, do not change with time. In other words, the rate of flow through any cross section of a pipe in a steady flow is constant.
Unsteady flow
Fluid flow is said to be unsteady if at any point in the flowing fluid any one or all the characteristics describing the behavior of a fluid such as pressure, density, velocity and temperature change with time. Unsteady flow is that type of flow, in which the fluid characteristics change with respect to time or in other words, the rate of flow through any cross-section of a pipe is not constant.
Uniform flow
Flow is said to be uniform, when the velocity of flow does not change either in magnitude or in direction at any point in a flowing fluid, for a given time. For example, the flow of liquids under pressure through long pipelines with a constant diameter is called uniform flow.
Non-uniform flow
Flow is said to be non-uniform, when there is a change in velocity of the flow at different points in a flowing fluid, for a given time. For example, the flow of liquids under pressure through long pipelines of varying diameter is referred to as non-uniform flow.
All these type of flows can exist independently of each other. So there can be any of the four combinations of flows possible:
1. Steady uniform flow
2. Steady non-uniform flow
3. Unsteady uniform flow
4. Unsteady non-uniform flow.
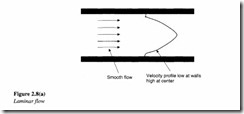
Laminar flow
A flow is said to be laminar if the fluid particles move in layers such that one layer of the fluid slides smoothly over an adjacent layer. The viscosity property of the fluid plays a significant role in the development of a laminar flow. The flow pattern exhibited by a highly viscous fluid may in general be treated as laminar flow (Figure 2.8(a)).
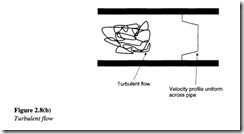
Turbulent flow
If the velocity of flow increases beyond a certain value, the flow becomes turbulent. As shown in Figure 2.8(b), the movement of fluid particles in a turbulent flow will be random. This mixing action of the colliding fluid particles generates turbulence, thereby resulting in more resistance to fluid flow and hence greater energy losses as compared to laminar flow.
The frictional resistance that a fluid moving in a pipe encounters, is normally proportional to the velocity of flow. However, once the flow turns turbulent, this frictional resistance encountered by the liquid becomes proportional to the square of the velocity of fluid flow.
Where
‘F’ is the resistance to fluid flow
‘v’ is the velocity of flow.
Due to greater energy losses, turbulent flow is generally avoided in hydraulic systems.
Some of the causes for turbulent flow in a hydraulic system are:
• Roughness of pipelines
• Obstructions to flow
• Degree of curvature of bends
• Increase in the number of bends.
Reynolds number
In a hydraulic system, it is important to know whether the flow pattern inside a pipe is laminar or turbulent and also to determine the conditions that govern the transition of the flow from laminar to turbulent. This is where Reynolds number holds much significance. The experiments performed by Osborn Reynolds led to important conclusions through which the nature of flow could be determined, by using a parameter known as the ‘Reynolds number’.
Reynolds number ‘Re’ is given by the expression:
Where
v is the velocity of flow
d is the diameter of the pipe
17 is the kinematic viscosity of the fluid.
Reynolds number is a pure ratio and is therefore dimensionless.
If Re is lesser than 2000, the flow is said to be laminar
If Re is greater than 4000, the flow is said to be turbulent.
Any value of Re ranging between 2000 and 4000 covers a critical zone between laminar and turbulent flow.
It is not possible to predict the type of flow within the critical zone. But normally,
turbulent flow should be assumed if the Reynolds number lies in the critical zone. As mentioned earlier, turbulent flow results in greater energy losses and therefore hydraulic systems should be designed to operate in the laminar flow region.
The greater energy losses that arise as a consequence of turbulent flow result in an increase in the temperature of the fluid. This condition can be alleviated to a great extent by providing for a slight increase in the pipe size in order to establish laminar flow.
Rotational flow
A flow is said to be rotational if the fluid particles moving in the direction of flow rotate around their own axis.
Non-rotational flow
If the fluid particles flowing in a laminar pattern do not rotate about their axis, then the flow is said to be non-rotational.
2.5.3 Rate of flow or discharge (Q)
The rate of flow or discharge is defined as the quantity of fluid flowing per second, through a pipe or channel section. In the case of incompressible fluids (liquids), the discharge is expressed in terms of the volume of fluid flowing across the section per second.
For compressible fluids (gases) the discharge is expressed as the weight of the fluid flowing across a section per second. So obviously the units of flow rate or discharge (Q) are: m3/s or liters/s for liquids and kgf/s or N/s for gases.
Consider a liquid flowing through a pipe of cross-sectional area ‘A’ and an average flow velocity ‘v’ across the section. We then have
Law of conservation of energy
As discussed earlier, the law of conservation of energy states that energy can neither be created nor destroyed, but can be transformed from one form to the other. This also means that the total energy of the system at any location remains constant.
The total energy of a liquid in motion includes:
• Potential energy
• Kinetic energy and
• Internal energy.
Potential energy (PE)
It is the energy stored in the system due to its position in the gravitational force field. If a heavy object such as building stone is lifted from the ground to the roof, the energy required to lift the stone is stored in it as potential energy. This stored potential energy remains unchanged as long as the stone remains in position.
Potential energy can be mathematically represented as:
Internal energy
Molecules possess mass. They also possess motion which is translational and rotational in nature, in both the liquid as well as the gaseous states. Owing to this mass and motion,
these molecules have a large amount of kinetic energy stored in them. Any change in temperature result s in a change in the molecular kinetic energy since molecular velocity is a function of temperature.
Also the molecules are attracted towards each other by very large forces in their solid state. These forces tend to vanish once a perfect gas state is reached. During the melting process of a solid or the vaporization process of a liquid, it is necessary to overcome these forces. The energy required .to bring about this change is stored in the molecules as potential energy .
The sum of these energies is called the internal energy, which is stored within the body. We refer to this energy as internal energy or thermal energy and it is denoted by the symbol ‘u’.
Bernoulli’s equation
An important equation formulated by an eighteenth-century Swiss scientist Daniel Bernoulli and known as Bernoulli’s equation is one of the vital tools employed in the analysis of hydraulic systems. By applying this principle in the design of a hydraulic system, it is possible to size various components comprising the system such as pumps, valves and piping, for effective and proper system operation.
Bernoulli’s equation basically enunciating the principle of conservation of energy states that in a liquid flowing continuously, the sum total of static, pressure and velocity energy heads is constant at all sections of the flow. The law as applied to a hydraulic pipeline is illustrated in Figure 2.9.
When this fluid arrives at section 2, assume that its elevation is ‘Z2 ‘, velocity is V2, and pressure is P2
According to Bernoulli’s principle, total energy possessed by the fluid at section 1 = Total energy possessed by the fluid at section 2
Since liquids are considered to be incompressible the density is the same and therefore the equation for a fluid of unit weight reduces to:
The use of the expression ‘head’ has gained widespread acceptance and accordingly Z is called the elevation or potential head
PIp is called the pressure head and
v2/2g is called the velocity head.
Further corrections to the above equation can be made by taking into account the following factors:
1. The frictional resistance to motion when the fluid passes through the pipe from section 1 to section 2 in overcoming which, a part of the fluid energy is lost. Let hr represent the energy head lost due to friction in the pipeline.
2. Assuming the presence of a pump and a motor between sections 1 and 2.
Let hp known as pump head represent the energy per unit weight of the fluid added by the pump and hm known as motor head represent the energy per unit weight utilized or removed by the motor. This leads us to the corrected Bernoulli’s equation which is
We shall now discuss the means by which the magnitude of the head loss can be evaluated.
The total head loss in the system can be further categorized as:
• Losses occurring in pipes and
• Losses occurring in fittings.
Head losses due to friction in pipes can be found by using the Darcy’s equation,which is
Where
f is Darcy’s frictional coefficient or factor
L is the length of the pipe
v is the average fluid velocity
d is the inside pipe diameter
g is the acceleration due to gravity.
Darcy’s equation can be applied for calculating the head loss due to friction, for both laminar as well as turbulent flows. The only difference will be in the evaluation of the frictional coefficient ‘f ‘.
Frictional losses in laminar flow
For laminar flow, the friction factor ‘f’ is given by
which is called the Hagen-Poiseuille equation.
Frictional losses in turbulent flow
Unlike in the case of laminar flow, the friction factor cannot be represented by a simple formula for turbulent flow. This is due to the fact that the movement of fluid particles in a turbulent flow is random and fluctuating in nature. Here the friction factor has been found to depend not only on the Reynolds number but also the relative roughness of the pipe. This relative roughness is given by:
The absolute roughness depends on the pipe material as well as the method of manufacture. Another point to be noted is that the roughness values of pipes undergo significant changes over a period of time due to deposit buildup on the walls.
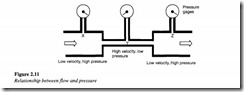
Pressure-flow relationship
Figure 2.11 shows a venturi essentially consisting of the following three sections:
1. Converging part
2. Throat and
3. Diverging part.
Let ‘vi’ and ‘v2 ‘ be the velocities of the fluid at the converging part which is section 1 and the throat which is section 2, respectively. From the continuity equation, we know that the flow velocity at the throat ‘v2 ‘ is greater than ‘vi’· Bernoulli’s equation for the flow between sections 1 and 2 can be written as
Since the pipe is horizontal, potential energy at both the sections is constant. Note that whenever the flow lines are located with a small difference in level, the potential head can be neglected.
Now, since v2 is greater than v . the pressure PI must be greater than P2 • This is in accordance with the law of conservation of energy, because if the fluid has gained kinetic energy by passing from section 1 to section 2, then it has to lose pressure energy in order to conform to the law of conservation of energy. Again, at the diverging portion of the pipe, the pressure recovers and the flow velocity falls.