Single phase flow
The flow of air only through a pipeline was considered in some detail in Chapter 10. This information is required since the pressure drop required to transport the air through the pipeline, without material, represents the datum for the pipeline. The air supply pressure available, minus the air only pressure drop for the pipeline, represents the pressure drop available for the conveying of material through the pipeline.
The Darcy equation for pressure drop
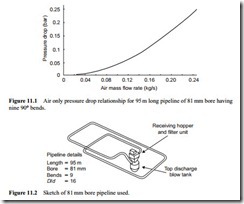
In order to illustrate how conveying characteristics can be used it is necessary to show first how they are built up and to examine the influence of the main variables. The simplest starting point is to consider the air only flowing through the pipeline. If a graph is drawn of pressure drop against air flow rate for the conveying line the result will be similar to that shown in Figure 11.1.
Top discharge blow tank
The data in Figure 11.1 relates to a 95 m long pipeline of 81 mm (3 in. nominal) bore that includes nine 90° bends. A sketch of the pipeline is given in Figure 11.2. This pipeline was used for conveying many of the materials for which conveying characteristics are presented here and so both the pipeline and Figure 11.1 will serve as a ref- erence to much of the data that follows.
This is single phase flow and the analysis of such flows is well established and quite straightforward. The pressure drop, !1pa, for a fluid (typically air) of density, p, flow- ing through a pipeline of a given diameter, d, and length, L, can be determined from Darcy’s Equation. This was presented in Equation (10.2) and is reproduced here for reference because of its importance:
where f is the pipeline friction factor (–) and C, the mean velocity of air (m/s).
It can be seen from this mathematical model that pressure drop follows a square law relationship with respect to velocity. This means that if the velocity is doubled the pres- sure drop will increase by a factor of four. Velocity, therefore, is a very important parameter in this work and constant reference will be made to this fact. As a consequence, in graphical representations of experimental results and data, velocity needs to be represented on one of the axes.
The use of air mass flow rate
A major problem with using velocity, however, is that it is not an independent variable. Gases are compressible and their densities vary with both pressure and temperature, as considered in some detail in Chapter 9. In Figure 11.1, it will be noticed that air mass flow rate has been used instead of velocity. Air mass flow rate is an independent variable and is an ideal substitute for velocity in this work.
Since density decreases with decrease in pressure, the velocity of the conveying gas will gradually increase along the length of a constant bore pipeline, but the mass flow rate of the gas will remain essentially constant. Velocity, C, can be determined quite
easily from the mass flow rate, m. a, using the Ideal Gas Law. This was presented in Equation (9.4) and is reproduced here for reference because of its importance:
where p is the absolute pressure of gas (kN/m2); V, the volumetric flow rate (m3/s);
m. a, the mass flow rate of gas (kg/s); T, the absolute temperature (K) and R, the characteristic gas constant (kJ/kg · K).
This was developed into an expression from which the conveying line inlet air velocity, C1, could be evaluated, for a circular pipe with air as the conveying gas, in Equation (9.20) and this is reproduced below for reference:
Conveying line exit air velocity, C2, can be similarly evaluated with values of T2, and p2.
This shows quite clearly how velocity is influenced by both gas pressure and temperature for a constant mass flow rate, and that for any given set of conveying conditions the air velocity can be evaluated quite easily.
Gas–solid flows
Figure 11.1 represents the relationship between air flow rate and pressure drop for the pipeline in Figure 11.2. If a small quantity of a granular or powdered material is fed into the air in the pipeline at a steady rate there will be an increase in the conveying line pressure drop, if the mass flow rate of the air remains constant. The magnitude of this increase depends upon the concentration of the material in the air.
The influence of conveyed solids on pressure drop
In a two phase flow system consisting of air and solid particles conveyed in suspension, part of the pressure drop is due to the air alone and part is due to the conveying of the
particles in the air stream. In such a two phase flow the particles are conveyed at a velocity below that of the conveying gas, as considered in Section 1.2.3.4. There is, therefore, a drag force exerted on the particles by the air.
The influence of particle concentration on conveying line pressure drop over a wide range of conveying air mass flow rates, and hence velocities, is illustrated in Figure 11.3. The material conveyed here is potassium chloride having a mean particle size of about 500 j.Lm. Conveying line pressure drop is plotted against air mass flow rate and lines of constant material flow rate are drawn on the graph.
The zero line at the bottom of the graph is the curve representing the variation of conveying line pressure drop with air flow rate for air only that comes from Figure 11.1. This, therefore, represents the lower limit with respect to material conveying capacity for the given system. It has been reported that the air only pressure drop curve can be reduced below the value shown on Figure 11.1 with ‘seeding’ of the pipeline. This is a boundary layer effect that can be achieved with low flow rates of particles. The material flow rates, however, are very low and are not appropriate to pneumatic conveying.
The curves drawn on Figure 11.3 were obtained from tests carried out with the material conveyed through the 81 mm bore conveying line shown in Figure 11.2. The data on Figure 11.3, therefore, relates only to the material tested and to this particular pipeline. This aspect of the problem is considered in more detail later.
Evaluation of velocity
If the superficial conveying air velocity is required for any condition this can be deter- mined for any given air mass flow rate quite simply from the model in Equation (11.3). For the 81 mm bore pipeline over the range of air mass flow rates and pressures on Figure 11.3 this is shown in Figure 11.4. The relationships presented are for air at a tem- perature of 20°C.
For low pressure dilute phase conveying systems positive displacement blowers are often used, but their maximum delivery pressure capability is typically about 1 bar gauge. These are essentially adiabatic machines and so the air can reach quite high temperatures at outlet. The influence of temperature on conveying air velocity, for both air and material, is considered at Section 9.6.
Conveying limitations
Apart from the lower limit of zero for material conveying capacity, there are three other limitations on the plot in Figure 11.3. The first is the limit on the right hand side of the graph. This is not, in fact, a limit at all and conveying is possible with much higher air flow rates. In the case presented it was set by the volumetric capacity of the com- pressor used. By reference to Figure 11.4, however, it will be seen that conveying air velocities are up to about 40 m/s and for the majority of pneumatic conveying systems this is considered to be the upper limit.
The upper limit on air flow rate is influenced partly by problems of particle degradation and bend erosion in the conveying line, but it is mainly due to the adverse effect on the conveying line pressure drop and hence material flow rate. This relates to the influence of the (velocity)2 term on pressure drop in Equation (11.1), that also applies approxi- mately to gas–solid flows at high values of velocity. In terms of the overall conveying characteristics, the shape of the curves is quite clearly established within this maximum limit.
The second limit is that at the top of the graph. Once again, this is not a limit at all and conveying will be possible with very much higher pressures. In the case presented it was set by the pressure rating of the compressor used. For the type of material conveyed, however, it is also set by the flow rate of the air. Since the material can only be conveyed in suspension flow, at high velocity, the air flow rate available is close to its limit at a pressure of 1.2 bar gauge.
The third limit is that on the left hand side of the graph and this represents the approxi- mate safe minimum conditions for successful conveying with the material. The lines actually terminate and conveying is not possible in the area to the left at lower air mass flow rates.
This limit is influenced by a complex combination of material properties, material concentration and conveying distance. In Figure 11.3 the potassium chloride is conveyed in dilute phase or suspension flow partly because the conveying line pressure gradient is very low, that is the ratio of the conveying line pressure drop to the pipeline length. As a result, a relatively high minimum conveying air velocity is required for this material.
Any attempt to convey with a lower air flow rate would result in blockage of the pipeline, in a conventional conveying system. This is because the air flow rate would be below the minimum required to keep the material in suspension. The terminology employed for these situations is choking, when conveying vertically up, and saltation when conveying horizontally.
It will be noted in Figure 11.3 that the lines of constant material flow rate terminate at progressively higher air mass flow rates as the material flow rate increases. This does not mean that the minimum conveying air velocity increases. This is entirely due to the influence of air pressure and, by reference to Figure 11.4, it will be seen that the minimum conveying air velocity for this material is about 15 m/s and that it changes little over this range of material flow rates.
At much higher material concentrations, or solids loading ratios, the minimum conveying velocity can be very much lower for materials having good air retention proper- ties. This, however, is non-suspension flow, or the dense phase region, where the mode of conveying is very different.
Conveying air velocity effects
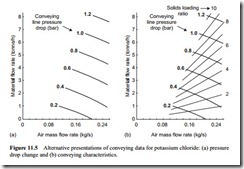
An alternative way of presenting the data is to plot the material flow rate against the air flow rate and to have a series of curves at a constant value of the conveying line pressure drop. Such a plot is shown in Figure 11.5a. This shows the influence of excessively high conveying air velocities which result in the lines of constant pressure drop sloping quite steeply to the air flow rate axis, and hence to zero material flow rate, at very high velocities.
This is because of the square law relationship of pressure drop with respect to velocity, as mentioned above. If the conveying system has a compressor or blower with a maximum rating in terms of delivery pressure, a considerable amount of this available pressure will be taken up by moving the air through the line if the air flow rate, and hence velocity, is too high.
Part of the pressure drop is due to the material being conveyed and the greater the concentration of the material in the air, the greater the pressure drop. If the conveying air velocity is too high, therefore, the concentration of the material in the air will have to be reduced in order to match the available pressure drop, and so the resulting material flow rate will be much lower.
Solids loading ratio
Solids loading ratio is the term generally used by pneumatic conveying engineers to describe the conveyed gas–solids flow. Solids loading ratio is the ratio of the mass flow rate of the solids conveyed to the mass flow rate of the air used (see Equation (1.3)). The particular advantages over particle concentration are that it is a dimensionless quan- tity and its value does not vary with the conveying gas pressure. With the graphs in Figure 11.5 being plots of material flow rate against air flow rate, lines of constant solids loading ratio can be superimposed quite easily as they are straight lines through the origin. Such a plot is shown in Figure 11.5b.