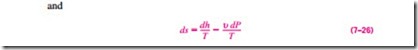■ THE T ds RELATIONS
Recall that the quantity (dQ/T)int rev corresponds to a differential change in a property, called entropy. The entropy change for a process, then, was evaluated by integrating dQ/T along some imaginary internally reversible path between the actual end states. For isothermal internally reversible processes, this integration is straightforward. But when the temperature varies during the process, we have to have a relation between dQ and T to perform this integration. Finding such relations is what we intend to do in this section.
The differential form of the conservation of energy equation for a closed stationary system (a fixed mass) containing a simple compressible substance can be expressed for an internally reversible process as
Equations 7–23 and 7–24 are extremely valuable since they relate entropy changes of a system to the changes in other properties. Unlike Eq. 7–4, they are property relations and therefore are independent of the type of the processes.
These T ds relations are developed with an internally reversible process in mind since the entropy change between two states must be evaluated along a reversible path. However, the results obtained are valid for both reversible and irreversible processes since entropy is a property and the change in a property between two states is independent of the type of process the system under- goes. Equations 7–23 and 7–24 are relations between the properties of a unit mass of a simple compressible system as it undergoes a change of state, and they are applicable whether the change occurs in a closed or an open system (Fig. 7–28).
Explicit relations for differential changes in entropy are obtained by solving for ds in Eqs. 7–23 and 7–24:
The entropy change during a process can be determined by integrating either of these equations between the initial and the final states. To perform these integrations, however, we must know the relationship between du or dh and the temperature (such as du = Cu dT and dh = Cp dT for ideal gases) as well as the equation of state for the substance (such as the ideal-gas equation of state Pu = RT). For substances for which such relations exist, the integration of Eq. 7–25 or 7–26 is straightforward. For other substances, we have to rely on tabulated data.
The T ds relations for nonsimple systems, that is, systems that involve more than one mode of quasi-equilibrium work, can be obtained in a similar manner by including all the relevant quasi-equilibrium work modes.