THE INCREASE OF ENTROPY PRINCIPLE
Consider a cycle that is made up of two processes: process 1-2, which is arbitrary (reversible or irreversible), and process 2-1, which is internally reversible, as shown in Fig. 7–5. From the Clausius inequality,
where the equality holds for an internally reversible process and the inequality for an irreversible process. We may conclude from these equations that the entropy change of a closed system during an irreversible process is greater than the integral of dQ/T evaluated for that process. In the limiting case of a reversible process, these two quantities become equal. We again emphasize that T in these relations is the absolute temperature at the boundary where the differential heat dQ is transferred between the system and the surroundings.
The quantity !::S = S2 – S1 represents the entropy change of the system. For a reversible process, it becomes equal to f21 dQ/T, which represents the entropy transfer with heat.
The inequality sign in the preceding relations is a constant reminder that the entropy change of a closed system during an irreversible process is always greater than the entropy transfer. That is, some entropy is generated or created during an irreversible process, and this generation is due entirely to the pres- ence of irreversibilities. The entropy generated during a process is called entropy generation and is denoted by Sgen. Noting that the difference between the entropy change of a closed system and the entropy transfer is equal to entropy generation, Eq. 7–7 can be rewritten as an equality as
Note that the entropy generation Sgen is always a positive quantity or zero. Its value depends on the process, and thus it is not a property of the system. Also, in the absence of any entropy transfer, the entropy change of a system is equal to the entropy generation.
Equation 7–7 has far-reaching implications in thermodynamics. For an iso- lated system (or simply an adiabatic closed system), the heat transfer is zero, and Eq. 7–7 reduces to
This equation can be expressed as the entropy of an isolated system during a process always increases or, in the limiting case of a reversible process, re- mains constant. In other words, it never decreases. This is known as the in- crease of entropy principle. Note that in the absence of any heat transfer, entropy change is due to irreversibilities only, and their effect is always to in- crease entropy.
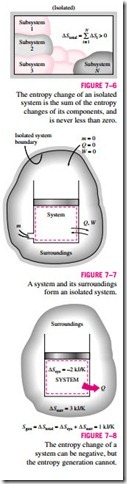
Entropy is an extensive property, and thus the total entropy of a system is equal to the sum of the entropies of the parts of the system. An isolated system may consist of any number of subsystems (Fig. 7–6). A system and its sur- roundings, for example, constitute an isolated system since both can be en-closed by a sufficiently large arbitrary boundary across which there is no heat, work, or mass transfer (Fig. 7–7). Therefore, a system and its surroundings can be viewed as the two subsystems of an isolated system, and the entropy change of this isolated system during a process is the sum of the entropy changes of the system and its surroundings, which is equal to the entropy generation since an isolated system involves no entropy transfer. That is,
where the equality holds for reversible processes and the inequality for ir- reversible ones. Note that !::Ssurr refers to the change in the entropy of the surroundings as a result of the occurrence of the process under consideration.
Since no actual process is truly reversible, we can conclude that some en- tropy is generated during a process, and therefore the entropy of the universe, which can be considered to be an isolated system, is continuously increasing. The more irreversible a process, the larger the entropy generated during that process. No entropy is generated during reversible processes (Sgen = 0).
Entropy increase of the universe is a major concern not only to engineers but also to philosophers, theologians, economists, and environmentalists since entropy is viewed as a measure of the disorder (or “mixed-up-ness”) in the universe.
The increase of entropy principle does not imply that the entropy of a system cannot decrease. The entropy change of a system can be negative during a process (Fig. 7–8), but entropy generation cannot. The increase of entropy principle can be summarized as follows:
This relation serves as a criterion in determining whether a process is reversible, irreversible, or impossible.
Things in nature have a tendency to change until they attain a state of equilibrium. The increase of entropy principle dictates that the entropy of an isolated system will increase until the entropy of the system reaches a maximum value. At that point, the system is said to have reached an equilibrium state since the increase of entropy principle prohibits the system from undergoing any change of state that will result in a decrease in entropy.
Some Remarks about Entropy
In light of the preceding discussions, we can draw these conclusions:
1. Processes can occur in a certain direction only, not in any direction.
A process must proceed in the direction that complies with the increase of entropy principle, that is, Sgen > 0. A process that violates this principle is impossible. This principle often forces chemical reactions to come to a halt before reaching completion.
2. Entropy is a nonconserved property, and there is no such thing as
the conservation of entropy principle. Entropy is conserved during the idealized reversible processes only and increases during all actual processes. Therefore, the entropy of the universe is continuously increasing.
3. The performance of engineering systems is degraded by the presence of irreversibilities, and entropy generation is a measure of the magnitudes of the irreversibilities present during that process. The greater the extent of irreversibilities, the greater the entropy generation. Therefore, entropy generation can be used as a quantitative measure of irreversibilities associated with a process. It is also used to establish criteria for the performance of engineering devices. This point is illustrated further in Example 7–2.
Incoming search terms:
- principle of increase of entropy
- principle of entropy increase
- increase of entropy principle
- principle of increase in entropy
- state principle ofincrease of entropy
- principle of entrophy increase
- Principle of the increase of Entropy
- principles of increase of entropy
- prove the increse of entropy principle
- Prove the principle of the increase of entropy
- state and prove principle of increase of entropy
- the principle of increase of entropy
- entropy principle of increase of entrophy
- principle of incease of entropy
- PRINCIPLE OF ENTROPY INCREASE FOR SYSTEM AND SURROUNDINGS
- principle of entropy generation
- principle behind increase in entropy
- principal increase of entrophy
- explain the principle of increases of entropy
- explain the principle of increase of entropy
- example of priciple of increase in entropy
- what is principle of entropy#spf=1