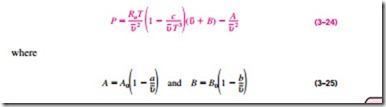OTHER EQUATIONS OF STATE
The ideal-gas equation of state is very simple, but its range of applicability is limited. It is desirable to have equations of state that represent the P-υ-T behavior of substances accurately over a larger region with no limitations.
Such equations are naturally more complicated. Several equations have been proposed for this purpose (Fig. 3–57), but we shall discuss only three: the van der Waals equation because it is one of the earliest, the Beattie-Bridgeman equation of state because it is one of the best known and is reasonably ac- curate, and the Benedict-Webb-Rubin equation because it is one of the more recent and is very accurate.
Van der Waals Equation of State
The van der Waals equation of state was proposed in 1873, and it has two constants that are determined from the behavior of a substance at the critical point. It is given by
Van der Waals intended to improve the ideal-gas equation of state by including two of the effects not considered in the ideal-gas model: the inter- molecular attraction forces and the volume occupied by the molecules them-sure and temperature, the volume actually occupied by molecules is only about one-thousandth of the volume of the room. As the pressure increases, the volume occupied by the molecules becomes an increasingly significant part of the total volume. Van der Waals proposed to correct this by replacing υ in the ideal-gas relation with the quantity υ – b, where b represents the volume occupied by the gas molecules per unit mass.
The determination of the two constants appearing in this equation is based on the observation that the critical isotherm on a P-υ diagram has a horizontal inflection point at the critical point (Fig. 3–58). Thus, the first and the second derivatives of P with respect to υ at the critical point must be zero. That is,
By performing the differentiations and eliminating υcr, the constants a and b are determined to be
The constants a and b can be determined for any substance from the critical- point data alone (Table A–1).
The accuracy of the van der Waals equation of state is often inadequate, but it can be improved by using values of a and b that are based on the actual behavior of the gas over a wider range instead of a single point. Despite its limitations, the van der Waals equation of state has a historical value in that it was one of the first attempts to model the behavior of real gases. The van der Waals equation of state can also be expressed on a unit-mole basis by replacing the υ in Eq. 3–22 by and the R in Eqs. 3–22 and 3–23 by Ru.
Beattie-Bridgeman Equation of State
The Beattie-Bridgeman equation, proposed in 1928, is an equation of state based on five experimentally determined constants. It was proposed as
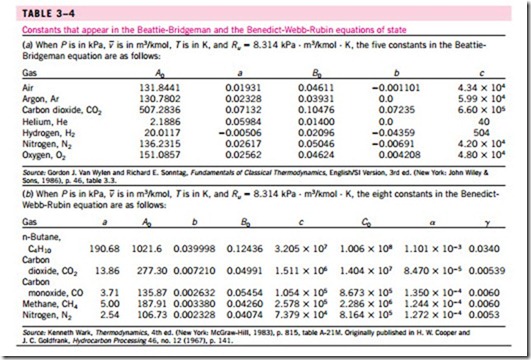
The constants appearing in the above equation are given in Table 3–4 for various substances. The Beattie-Bridgeman equation is known to be reasonably accurate for densities up to about 0.8rcr, where rcr is the density of the sub- stance at the critical point.
Benedict-Webb-Rubin Equation of State
Benedict, Webb, and Rubin extended the Beattie-Bridgeman equation in 1940 by raising the number of constants to eight. It is expressed as
The values of the constants appearing in this equation are given in Table 3–4. This equation can handle substances at densities up to about 2.5rcr. In 1962, Strobridge further extended this equation by raising the number of constants to 16 (Fig. 3–59).
Virial Equation of State
The equation of state of a substance can also be expressed in a series form as
This and similar equations are called the virial equations of state, and the coefficients a(T ), b(T ), c(T ), and so on, that are functions of temperature alone are called virial coefficients. These coefficients can be determined experimentally or theoretically from statistical mechanics. Obviously, as the pressure approaches zero, all the virial coefficients will vanish and the equation will reduce to the ideal-gas equation of state. The P-u–T behavior of a sub- stance can be represented accurately with the virial equation of state over a wider range by including a sufficient number of terms. The equations of state discussed here are applicable to the gas phase of the substances only, and thus should not be used for liquids or liquid–vapor mixtures.
Complex equations represent the P-u-T behavior of substances reasonably well and are very suitable for digital computer applications. For hand calculations, however, it is suggested that the reader use the property tables or the simpler equations of state for convenience. This is particularly true for specific-volume calculations since all the earlier equations are implicit in u and will require a trial-and-error approach. The accuracy of the van der Waals,
Incoming search terms:
- applicability of vanderwalls equation
- at what condition beattie bridgeman equation becomes reasonably accurate