TEMPERATURE AND THE ZEROTH LAW OF THERMODYNAMICS
Although we are familiar with temperature as a measure of “hotness” or “coldness,” it is not easy to give an exact definition for it. Based on our phys- iological sensations, we express the level of temperature qualitatively with words like freezing cold, cold, warm, hot, and red-hot. However, we cannot assign numerical values to temperatures based on our sensations alone. Fur- thermore, our senses may be misleading. A metal chair, for example, will feel much colder than a wooden one even when both are at the same temperature. Fortunately, several properties of materials change with temperature in a repeatable and predictable way, and this forms the basis for accurate temperature measurement. The commonly used mercury-in-glass thermometer, for example, is based on the expansion of mercury with temperature. Temperature is also measured by using several other temperature-dependent properties.
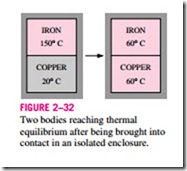
It is a common experience that a cup of hot coffee left on the table eventu- ally cools off and a cold drink eventually warms up. That is, when a body is brought into contact with another body that is at a different temperature, heat is transferred from the body at higher temperature to the one at lower temper- ature until both bodies attain the same temperature (Fig. 2–32). At that point, the heat transfer stops, and the two bodies are said to have reached thermal equilibrium. The equality of temperature is the only requirement for thermal equilibrium.
The zeroth law of thermodynamics states that if two bodies are in thermal equilibrium with a third body, they are also in thermal equilibrium with each other. It may seem silly that such an obvious fact is called one of the basic laws of thermodynamics. However, it cannot be concluded from the other laws of thermodynamics, and it serves as a basis for the validity of tempera- ture measurement. By replacing the third body with a thermometer, the zeroth law can be restated as two bodies are in thermal equilibrium if both have the same temperature reading even if they are not in contact.
The zeroth law was first formulated and labeled by R. H. Fowler in 1931. As the name suggests, its value as a fundamental physical principle was rec- ognized more than half a century after the formulation of the first and the sec- ond laws of thermodynamics. It was named the zeroth law since it should have preceded the first and the second laws of thermodynamics.
Temperature Scales
Temperature scales enable us to use a common basis for temperature measurements, and several have been introduced throughout history. All temperature scales are based on some easily reproducible states such as the freezing and boiling points of water, which are also called the ice point and the steam point, respectively. A mixture of ice and water that is in equilibrium with air saturated with vapor at 1 atm pressure is said to be at the ice point, and a mixture of liquid water and water vapor (with no air) in equilibrium at 1 atm pressure is said to be at the steam point.
The temperature scales used in the SI and in the English system today are the Celsius scale (formerly called the centigrade scale; in 1948 it was re- named after the Swedish astronomer A. Celsius, 1702–1744, who devised it) and the Fahrenheit scale (named after the German instrument maker
G. Fahrenheit, 1686–1736), respectively. On the Celsius scale, the ice and steam points are assigned the values of 0 and 100°C, respectively. The corresponding values on the Fahrenheit scale are 32 and 212°F. These are often referred to as two-point scales since temperature values are assigned at two different points.
In thermodynamics, it is very desirable to have a temperature scale that is independent of the properties of any substance or substances. Such a tem- perature scale is called a thermodynamic temperature scale, which is de- veloped later in conjunction with the second law of thermodynamics. The thermodynamic temperature scale in the SI is the Kelvin scale, named after Lord Kelvin (1824–1907). The temperature unit on this scale is the kelvin, which is designated by K (not °K; the degree symbol was officially dropped from kelvin in 1967). The lowest temperature on the Kelvin scale is 0 K. Using nonconventional refrigeration techniques, scientists have approached absolute zero kelvin (they achieved 0.000000002 K in 1989).
The thermodynamic temperature scale in the English system is the Rankine scale, named after William Rankine (1820–1872). The temperature unit on this scale is the rankine, which is designated by R.
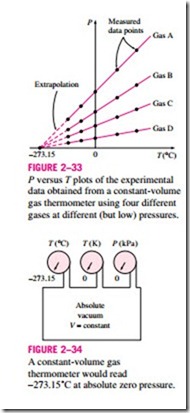
A temperature scale that turns out to be identical to the Kelvin scale is the ideal-gas temperature scale. The temperatures on this scale are measured using a constant-volume gas thermometer, which is basically a rigid vessel filled with a gas, usually hydrogen or helium, at low pressure. This ther- mometer is based on the principle that at low pressures, the temperature of a gas is proportional to its pressure at constant volume. That is, the temperature of a gas of fixed volume varies linearly with pressure at sufficiently low pressures. Then the relationship between the temperature and the pressure of the gas in the vessel can be expressed as
where the values of the constants a and b for a gas thermometer are deter- mined experimentally. Once a and b are known, the temperature of a medium can be calculated from this relation by immersing the rigid vessel of the gas thermometer into the medium and measuring the gas pressure when thermal equilibrium is established between the medium and the gas in the vessel whose volume is held constant.
An ideal 1-1 gas temperature scale can be developed by measuring the pressures of the gas in the vessel at two reproducible points (such as the ice and the steam points) and assigning suitable values to temperatures at those two points. Considering that only one straight line passes through two fixed points on a plane, these two measurements are sufficient to determine the constants a and b in Eq. 2–11. Then the unknown temperature T of a medium corresponding to a pressure reading P can be determined from that equation by a simple calculation. The values of the constants will be different for each thermometer, depending on the type and the amount of the gas in the vessel, and the temperature values assigned at the two reference points. If the ice and steam points are assigned the values 0 and 100, respectively, then the gas temperature scale will be identical to the Celsius scale. In this case the value of the constant a (which corresponds to an absolute pressure of zero) is deter- mined to be -273.15˚C regardless of the type and the amount of the gas in the vessel of the gas thermometer. That is, on a P-T diagram, all the straight lines passing through the data points in this case will intersect the temperature axis at -273.15˚C when extrapolated, as shown in Fig. 2–33. This is the lowest temperature that can be obtained by a gas thermometer, and thus we can obtain an absolute gas temperature scale by assigning a value of zero to the con- stant a in Eq. 2–11. In that case Eq. 2–11 reduces to T = bP, and thus we need
It should be noted that the absolute gas temperature scale is not a thermodynamic temperature scale, since it cannot be used at very low temperatures (due to condensation) and at very high temperatures (due to dissociation and ionization). However, absolute gas temperature is identical to the thermodynamic temperature in the temperature range in which the gas thermometer can be used, and thus we can view the thermodynamic temperature scale at this point as an absolute gas temperature scale that utilizes an “ideal” or “imaginary” gas that always acts as a low-pressure gas regardless of the temperature. If such a gas thermometer existed, it would read zero kelvin at absolute zero pressure, which corresponds to -273.15°C on the Celsius scale (Fig. 2–34).
The Kelvin scale is related to the Celsius scale by
It is common practice to round the constant in Eq. 2–12 to 273 and that in Eq. 2–13 to 460.
The temperature scales in the two unit systems are related by
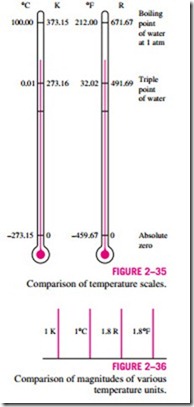
A comparison of various temperature scales is given in Fig. 2–35.
At the Tenth Conference on Weights and Measures in 1954, the Celsius scale was redefined in terms of a single fixed point and the absolute temperature scale. The selected single point is the triple point of water (the state at which all three phases of water coexist in equilibrium), which is assigned the value 0.01°C. The magnitude of the degree is defined from the absolute temperature scale. As before, the boiling point of water at 1 atm pressure is 100.00°C. Thus the new Celsius scale is essentially the same as the old one. On the Kelvin scale, the size of the temperature unit kelvin is defined as “the fraction 1/273.16 of the thermodynamic temperature of the triple point of water, which is assigned the value of 273.16 K.” The ice point on the Celsius and Kelvin scales are 0°C and 273.15 K, respectively.
Note that the magnitudes of each division of 1 K and 1°C are identical (Fig. 2–36). Therefore, when we are dealing with temperature differences T, the temperature interval on both scales is the same. Raising the temperature of a substance by 10°C is the same as raising it by 10 K. That is,
Some thermodynamic relations involve the temperature T and often the question arises of whether it is in K or °C. If the relation involves temperature differences (such as a = b T), it makes no difference and either can be used. However, if the relation involves temperatures only instead of temperature differences (such as a = bT) then K must be used. When in doubt, it is always safe to use K because there are virtually no situations in which the use of K is incorrect, but there are many thermodynamic relations that will yield an erroneous result if °C is used.