SPECIFIC HEATS
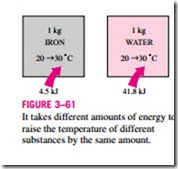
We know from experience that it takes different amounts of energy to raise the temperature of identical masses of different substances by one degree. For example, we need about 4.5 kJ of energy to raise the temperature of 1 kg of iron from 20 to 30°C, whereas it takes about 9 times this energy (41.8 kJ to be
exact) to raise the temperature of 1 kg of liquid water by the same amount (Fig. 3–61). Therefore, it is desirable to have a property that will enable us to compare the energy storage capabilities of various substances. This property is the specific heat.
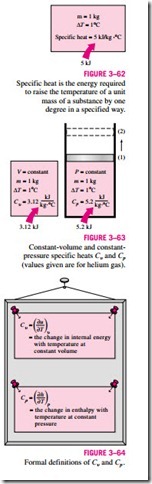
The specific heat is defined as the energy required to raise the temperature of a unit mass of a substance by one degree (Fig. 3–62). In general, this energy will depend on how the process is executed. In thermodynamics, we are inter- ested in two kinds of specific heats: specific heat at constant volume Cu and specific heat at constant pressure Cp.
Physically, the specific heat at constant volume Cu can be viewed as the energy required to raise the temperature of the unit mass of a substance by one degree as the volume is maintained constant. The energy required to do the same as the pressure is maintained constant is the specific heat at constant pressure Cp. This is illustrated in Fig. 3–63. The specific heat at constant pres- sure Cp is always greater than Cu because at constant pressure the system is allowed to expand and the energy for this expansion work must also be sup- plied to the system.
Now we will attempt to express the specific heats in terms of other thermo-dynamic properties. First, consider a fixed mass in a stationary closed system undergoing a constant-volume process (and thus no expansion or compression work is involved). The conservation of energy principle ein – eout = Llesystem for this process can be expressed in the differential form as
The left-hand side of this equation represents the net amount of energy transferred to the system. From the definition of Cu, this energy must be equal to Cu dT, where dT is the differential change in temperature. Thus,
Equations 3–28 and 3–29 are the defining equations for Cu and Cp, and their interpretation is given in Fig. 3–64.
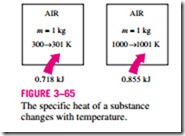
Note that Cu and Cp are expressed in terms of other properties; thus, they must be properties themselves. Like any other property, the specific heats of a substance depend on the state that, in general, is specified by two independent, intensive properties. That is, the energy required to raise the temperature of a substance by one degree will be different at different temperatures and pressures (Fig. 3–65). But this difference is usually not very large.
A few observations can be made from Eqs. 3–28 and 3–29. First, these equations are property relations and as such are independent of the type of processes. They are valid for any substance undergoing any process. The only relevance Cu has to a constant-volume process is that Cu happens to be the
energy transferred to a system during a constant-volume process per unit mass per unit degree rise in temperature. This is how the values of Cu are deter- mined. This is also how the name specific heat at constant volume originated. Likewise, the energy transferred to a system per unit mass per unit tempera- ture rise during a constant-pressure process happens to be equal to Cp. This is how the values of Cp can be determined and also explains the origin of the
0.718 kJ 0.855 kJ name specific heat at constant pressure.
Another observation that can be made from Eqs. 3–28 and 3–29 is that Cu is related to the changes in internal energy and Cp to the changes in enthalpy. In fact, it would be more proper to define Cu as the change in the internal energy of a substance per unit change in temperature at constant volume. Likewise, Cp can be defined as the change in the enthalpy of a substance per unit change in temperature at constant pressure. In other words, Cu is a measure of the variation of internal energy of a substance with temperature, and Cp is a mea- sure of the variation of enthalpy of a substance with temperature.
Both the internal energy and enthalpy of a substance can be changed by the transfer of energy in any form, with heat being only one of them. Therefore, the term specific energy is probably more appropriate than the term specific heat, which implies that energy is transferred (and stored) in the form of heat. A common unit for specific heats is kJ/kg · °C or kJ/kg · K. Notice that these two units are identical since DT(°C) = DT(K), and 1°C change in temperature is equivalent to a change of 1 K. The specific heats are sometimes given on a molar basis. They are then denoted by C u and C p and have the unit kJ/kmol · °C or kJ/kmol · K.