HEAT EXCHANGERS:THE EFFECTIVENESS–NTU METHOD

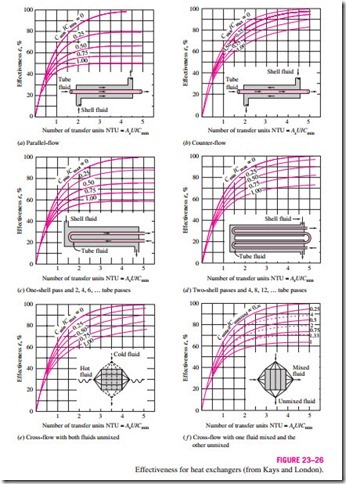
■ THE EFFECTIVENESS–NTU METHOD

The log mean temperature difference (LMTD) method discussed in Section 23–4 is easy to use in heat exchanger analysis when the inlet and the outlet temperatures of the hot and cold fluids are known or can be determined from an energy balance. Once /},Tlm, the mass flow rates, and the overall heat transfer coefficient are available, the heat transfer surface area of the heat ex- changer can be determined from

Therefore, the LMTD method is very suitable for determining the size of a heat exchanger to realize prescribed outlet temperatures when the mass flow rates and the inlet and outlet temperatures of the hot and cold fluids are specified.

With the LMTD method, the task is to select a heat exchanger that will meet the prescribed heat transfer requirements. The procedure to be followed by the selection process is:

1. Select the type of heat exchanger suitable for the application.

2. Determine any unknown inlet or outlet temperature and the heat transfer rate using an energy balance.

3. Calculate the log mean temperature difference /},Tlm and the correction factor F, if necessary.

4. Obtain (select or calculate) the value of the overall heat transfer co- efficient U.

5. Calculate the heat transfer surface area As .

The task is completed by selecting a heat exchanger that has a heat transfer surface area equal to or larger than As .

A second kind of problem encountered in heat exchanger analysis is the de- termination of the heat transfer rate and the outlet temperatures of the hot and cold fluids for prescribed fluid mass flow rates and inlet temperatures when the type and size of the heat exchanger are specified. The heat transfer surface area A of the heat exchanger in this case is known, but the outlet temperatures are not. Here the task is to determine the heat transfer performance of a specified heat exchanger or to determine if a heat exchanger available in storage will do the job.

The LMTD method could still be used for this alternative problem, but the procedure would require tedious iterations, and thus it is not practical. In an attempt to eliminate the iterations from the solution of such problems, Kays and London came up with a method in 1955 called the effectiveness–NTU method, which greatly simplified heat exchanger analysis.

This method is based on a dimensionless parameter called the heat trans- fer effectiveness e, defined as

where Cc = mcCpc and Ch = mcCph are the heat capacity rates of the cold and the hot fluids, respectively.

To determine the maximum possible heat transfer rate in a heat exchanger, we first recognize that the maximum temperature difference in a heat ex- changer is the difference between the inlet temperatures of the hot and cold fluids. That is,

The heat transfer in a heat exchanger will reach its maximum value when (1) the cold fluid is heated to the inlet temperature of the hot fluid or (2) the hot fluid is cooled to the inlet temperature of the cold fluid. These two limit- ing conditions will not be reached simultaneously unless the heat capacity rates of the hot and cold fluids are identical (i.e., Cc = Ch). When Cc * Ch, which is usually the case, the fluid with the smaller heat capacity rate will experience a larger temperature change, and thus it will be the first to experience the maximum temperature, at which point the heat transfer will come to a halt. Therefore, the maximum possible heat transfer rate in a heat exchanger is (Fig. 23–23)

Therefore, the effectiveness of a heat exchanger enables us to determine the heat transfer rate without knowing the outlet temperatures of the fluids.

The effectiveness of a heat exchanger depends on the geometry of the heat exchanger as well as the flow arrangement. Therefore, different types of heat exchangers have different effectiveness relations. Below we illustrate the de- velopment of the effectiveness e relation for the double-pipe parallel-flow heat exchanger.

Equation 23–23 developed in Section 23–4 for a parallel-flow heat ex- changer can be rearranged as

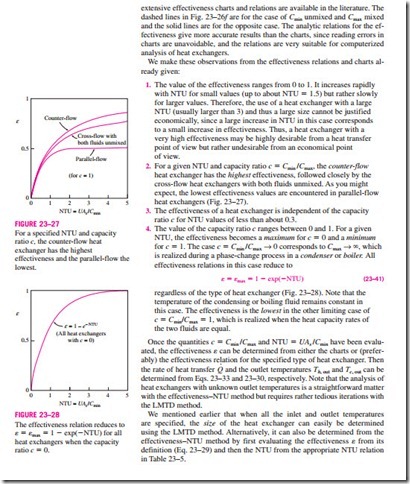
Effectiveness relations of the heat exchangers typically involve the dimensionless group UAs /Cmin. This quantity is called the number of transfer units NTU and is expressed as

where U is the overall heat transfer coefficient and As is the heat transfer surface area of the heat exchanger. Note that NTU is proportional to As . Therefore, for specified values of U and Cmin, the value of NTU is a measure of the heat trans- fer surface area As . Thus, the larger the NTU, the larger the heat exchanger.

In heat exchanger analysis, it is also convenient to define another dimensionless quantity called the capacity ratio c as

Effectiveness relations have been developed for a large number of heat ex- changers, and the results are given in Table 23–4. The effectivenesses of some common types of heat exchangers are also plotted in Fig. 23–26. More