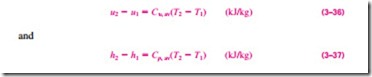INTERNAL ENERGY, ENTHALPY, AND SPECIFIC HEATS OF IDEAL GASES
We defined an ideal gas as a gas whose temperature, pressure, and specific volume are related by
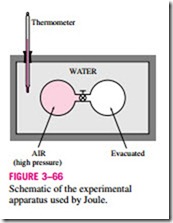
In his classical experiment, Joule submerged two tanks connected with a pipe and a valve in a water bath, as shown in Fig. 3–66. Initially, one tank contained air at a high pressure and the other tank was evacuated. When thermal equilibrium was attained, he opened the valve to let air pass from one tank to the other until the pressures equalized. Joule observed no change in the temperature of the water bath and assumed that no heat was transferred to or from the air. Since there was also no work done, he concluded that the internal energy of the air did not change even though the volume and the pressure changed. Therefore, he reasoned, the internal energy is a function of temperature only and not a function of pressure or specific volume. (Joule later Schematic of the experimental apparatus used by Joule.
showed that for gases that deviate significantly from ideal-gas behavior, the internal energy is not a function of temperature alone.)
Using the definition of enthalpy and the equation of state of an ideal gas, we have
To carry out these integrations, we need to have relations for Cu and Cp as functions of temperature.
At low pressures, all real gases approach ideal-gas behavior, and therefore their specific heats depend on temperature only. The specific heats of real gases at low pressures are called ideal-gas specific heats, or zero-pressure specific heats, and are often denoted Cp0 and Cu0. Accurate analytical expressions for ideal-gas specific heats, based on direct measurements or calculations from statistical behavior of molecules, are available and are given as third-degree polynomials in the appendix (Table A–2c) for several gases.
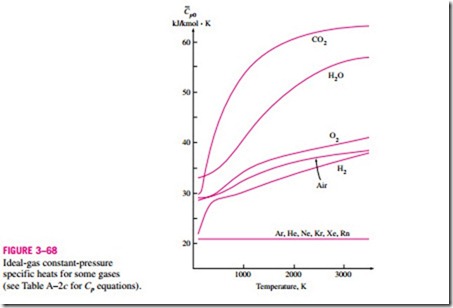
A plot of Cp0(T ) data for some common gases is given in Fig. 3–68.
The use of ideal-gas specific heat data is limited to low pressures, but these data can also be used at moderately high pressures with reasonable accuracy as long as the gas does not deviate from ideal-gas behavior significantly.
The integrations in Eqs. 3–34 and 3–35 are straightforward but rather time- consuming and thus impractical. To avoid these laborious calculations, u and h data for a number of gases have been tabulated over small temperature intervals. These tables are obtained by choosing an arbitrary reference point and performing the integrations in Eqs. 3–34 and 3–35 by treating state 1 as
the reference state. In the ideal-gas tables given in the appendix, zero kelvin is chosen as the reference state, and both the enthalpy and the internal energy are assigned zero values at that state (Fig. 3–69). The choice of the reference state has no effect on Du or Dh calculations. The u and h data are given in kJ/kg for air (Table A–21) and usually in kJ/kmol for other gases. The unit kJ/kmol is Some observations can be made from Fig. 3–68. First, the specific heats of gases with complex molecules (molecules with two or more atoms) are higher and increase with temperature. Also, the variation of specific heats with temperature is smooth and may be approximated as linear over small temperature intervals (a few hundred degrees or less). Then the specific heat functions in Eqs. 3–34 and 3–35 can be replaced by the constant average specific heat values. Now the integrations in these equations can be performed, yielding
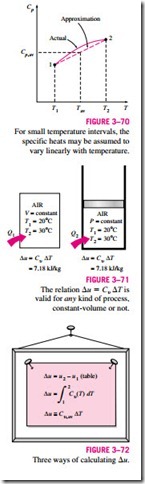
The specific heat values for some common gases are listed as a function of temperature in Table A–2b. The average specific heats Cp, av and Cu, av are evaluated from this table at the average temperature (T1 + T2)/2, as shown in Fig. 3–70. If the final temperature T2 is not known, the specific heats may be evaluated at T1 or at anticipated average temperature. Then T2 can be determined by using these specific heat values. The value of T2 can be refined, if necessary, by evaluating the specific heats at the new average temperature. Another way of determining the average specific heats is to evaluate them at T1 and T2 and then take their average. Usually both methods give reasonably good results, and one is not necessarily better than the other.
Another observation that can be made from Fig. 3–68 is that the ideal-gas specific heats of monatomic gases such as argon, neon, and helium remain constant over the entire temperature range. Thus, Du and Dh of monatomic gases can easily be evaluated from Eqs. 3–36 and 3–37.
Note that the Du and Dh relations given previously are not restricted to any kind of process. They are valid for all processes. The presence of the constant-
volume specific heat Cu in an equation should not lead one to believe that this equation is valid for a constant-volume process only. On the contrary, the relation Du = Cu, av DT is valid for any ideal gas undergoing any process (Fig. 3–71). A similar argument can be given for Cp and Dh.
To summarize, there are three ways to determine the internal energy and enthalpy changes of ideal gases (Fig. 3–72):
1. By using the tabulated u and h data. This is the easiest and most accurate way when tables are readily available.
2. By using the Cu or Cp relations as a function of temperature and performing the integrations. This is very inconvenient for hand
3. By using average specific heats. This is very simple and certainly very convenient when property tables are not available. The results obtained are reasonably accurate if the temperature interval is not very large.
Specific Heat Relations of Ideal Gases
The specific heat ratio also varies with temperature, but this variation is very mild. For monatomic gases, its value is essentially constant at 1.667. Many diatomic gases, including air, have a specific heat ratio of about 1.4 at room temperature.