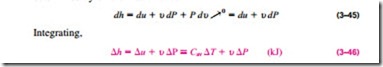INTERNAL ENERGY, ENTHALPY, AND SPECIFIC HEATS OF SOLIDS AND LIQUIDS
A substance whose specific volume (or density) is constant is called an in- compressible substance. The specific volumes of solids and liquids essentially remain constant during a process (Fig. 3–74). Therefore, liquids and solids can be approximated as incompressible substances without sacrificing much in accuracy. The constant-volume assumption should be taken to imply that the energy associated with the volume change is negligible compared with other forms of energy. Otherwise, this assumption would be ridiculous for studying the thermal stresses in solids (caused by volume change with temperature) or analyzing liquid-in-glass thermometers.
It can be mathematically shown that the constant-volume and constant- pressure specific heats are identical for incompressible substances (Fig. 3–75). Therefore, for solids and liquids, the subscripts on Cp and Cu can be dropped, and both specific heats can be represented by a single symbol C. That is,
This result could also be deduced from the physical definitions of constant- volume and constant-pressure specific heats. Specific heat values for several common liquids and solids are given in Table A–3.
Internal Energy Changes
Like those of ideal gases, the specific heats of incompressible substances depend on temperature only. Thus, the partial differentials in the defining equation of Cu can be replaced by ordinary differentials, which yield
Enthalpy Changes
Using the definition of enthalpy h = u + Pu and noting that u = constant, the differential form of the enthalpy change of incompressible substances can be
For solids, the term u LlP is insignificant and thus Llh = Llu � Cav LlT. For
liquids, two special cases are commonly encountered:
1. Constant-pressure processes, as in heaters
2. Constant-temperature processes, as in pumps
For a process between states 1 and 2, the last relation can be expressed as h2 – h1 = u(P2 – P1). By taking state 2 to be the compressed liquid state at a given T and P and state 1 to be the saturated liquid state at the same temperature, the enthalpy of the compressed liquid can be expressed as