A NOTE ON DIMENSIONS AND UNITS
Any physical quantity can be characterized by dimensions. The arbitrary magnitudes assigned to the dimensions are called units. Some basic dimensions such as mass m, length L, time t, and temperature T are selected as pri- mary or fundamental dimensions, while others such as velocity If, energy E, and volume V are expressed in terms of the primary dimensions and are called secondary dimensions, or derived dimensions.
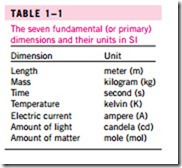
A number of unit systems have been developed over the years. Despite strong efforts in the scientific and engineering community to unify the world with a single unit system, two sets of units are still in common use today: the English system, which is also known as the United States Customary System (USCS), and the metric SI (from Le Système International d’ Unités), which is also known as the International System. The SI is a simple and logical system based on a decimal relationship between the various units, and it is being used for scientific and engineering work in most of the industrialized nations, including England. The English system, however, has no apparent systematic numerical base, and various units in this system are related to each other rather arbitrarily (12 in in 1 ft, 16 oz in 1 lb, 4 qt in 1 gal, etc.), which makes it confusing and difficult to learn. The United States is the only industrialized country that has not yet fully converted to the metric system. The systematic efforts to develop a universally acceptable system of units dates back to 1790 when the French National Assembly charged the French Academy of Sciences to come up with such a unit system. An early version of the metric system was soon developed in France, but it did not find universal acceptance until 1875 when The Metric Convection Treaty was prepared and signed by 17 nations, including the United States. In this international treaty, meter and gram were established as the metric units for length and mass, respectively, and a General Conference of Weights and Measures (CGPM) was established that was to meet every six years. In 1960, the CGPM pro- duced the SI, which was based on six fundamental quantities and their units were adopted in 1954 at the Tenth General Conference of Weights and Mea- sures: meter (m) for length, kilogram (kg) for mass, second (s) for time, am- pere (A) for electric current, degree Kelvin (°K) for temperature, and candela (cd) for luminous intensity (amount of light). In 1971, the CGPM added a seventh fundamental quantity and unit: mole (mol) for the amount of matter. Based on the notational scheme introduced in 1967, the degree symbol was officially dropped from the absolute temperature unit, and all unit names were to be written without capitalization even if they were derived from proper names (Table 1–1). However, the abbreviation of a unit was to be capitalized
if the unit was derived from a proper name. For example, the SI unit of force, which is named after Sir Isaac Newton (1647–1723), is newton (not Newton), and it is abbreviated as N. Also, the full name of a unit may be pluralized, but its abbreviation cannot. For example, the length of an object can be 5 m or 5 meters, not 5 ms or 5 meter. Finally, no period is to be used in unit abbreviations unless they appear at the end of a sentence. For example, the proper abbreviation of meter is m (not m.).
The recent move toward the metric system in the United States seems to have started in 1968 when Congress, in response to what was happening in the rest of the world, passed a Metric Study Act. Congress continued to promote a voluntary switch to the metric system by passing the Metric Conversion Act in 1975. A trade bill passed by Congress in 1988 set a September 1992 dead- line for all federal agencies to convert to the metric system. However, the deadlines were relaxed later with no clear plans for the future.
The industries that are heavily involved in international trade (such as the automotive, soft drink, and liquor industries) have been quick in converting to the metric system for economic reasons (having a single worldwide design, fewer sizes, smaller inventories, etc.). Today, nearly all the cars manufactured in the United States are metric. Most car owners probably do not realize this until they try an inch socket wrench on a metric bolt. Most industries, how- ever, resisted the change, thus slowing down the conversion process.
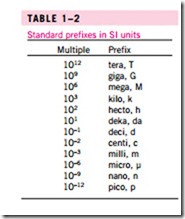
Presently the United States is a dual-system society, and it will stay that way until the transition to the metric system is completed. This puts an extra bur- den on today’s engineering students, since they are expected to retain their un- derstanding of the English system while learning, thinking, and working in terms of the SI. Given the position of the engineers in the transition period, both unit systems are used in this text, with particular emphasis on SI units. As pointed out earlier, the SI is based on a decimal relationship between units. The prefixes used to express the multiples of the various units are listed in Table 1–2. They are standard for all units, and the student is encouraged to memorize them because of their widespread use (Fig. 1–9).
Some SI and English Units
In SI, the units of mass, length, and time are the kilogram (kg), meter (m), and second (s), respectively. The respective units in the English system are the pound-mass (lbm), foot (ft), and second (s). The pound symbol lb is actually the abbreviation of libra, which was the ancient Roman unit of weight. The English retained this symbol even after the end of the Roman occupation of Britain in 410. The mass and length units in the two systems are related to each other by
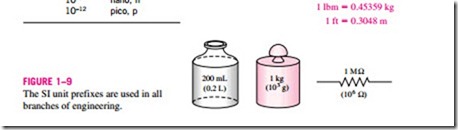
In the English system, force is usually considered to be one of the primary dimensions and is assigned a nonderived unit. This is a source of confusion and error that necessitates the use of a dimensional constant (gc) in many formulas. To avoid this nuisance, we consider force to be a secondary dimension whose unit is derived from Newton’s second law, i.e.,
In SI, the force unit is the newton (N), and it is defined as the force required to accelerate a mass of 1 kg at a rate of 1 m/s2. In the English system, the force unit is the pound-force (lbf ) and is defined as the force required to ac- celerate a mass of 32.174 lbm (1 slug) at a rate of 1 ft/s2 (Fig. 1–10). That is,
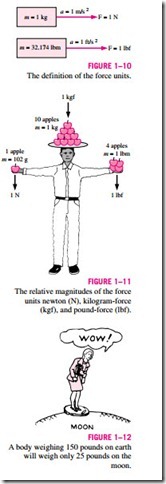
A force of 1 newton is roughly equivalent to the weight of a small apple (m = 102 g), whereas a force of 1 pound-force is roughly equivalent to the weight of 4 medium apples (mtotal = 454 g), as shown in Fig. 1–11. Another force unit in common use in many European countries is the kilogram-force (kgf), which is the weight of 1 kg mass at sea level (1 kgf = 9.807 N).
The term weight is often incorrectly used to express mass, particularly by the “weight watchers.” Unlike mass, weight W is a force. It is the gravitational force applied to a body, and its magnitude is determined from Newton’s sec- ond law,
where m is the mass of the body, and g is the local gravitational acceleration (g is 9.807 m/s2 or 32.174 ft/s2 at sea level and 45° latitude). The ordinary bathroom scale measures the gravitational force acting on a body. The weight of a unit volume of a substance is called the specific weight g and is deter- mined from g = rg, where r is density.
The mass of a body remains the same regardless of its location in the universe. Its weight, however, changes with a change in gravitational acceleration. A body will weigh less on top of a mountain since g decreases with altitude. On the surface of the moon, an astronaut weighs about one-sixth of what she or he normally weighs on earth (Fig. 1–12).
At sea level a mass of 1 kg weighs 9.807 N, as illustrated in Fig. 1–13. A mass of 1 lbm, however, weighs 1 lbf, which misleads people to believe that pound-mass and pound-force can be used interchangeably as pound (lb), which is a major source of error in the English system.
It should be noted that the gravity force acting on a mass is due to the at- traction between the masses, and thus it is proportional to the magnitudes of the masses and inversely proportional to the square of the distance between them. Therefore, the gravitational acceleration g at a location depends on the local density of the earth’s crust, the distance to the center of the earth, and to a lesser extent, the positions of the moon and the sun. The value of g varies with location from 9.8295 m/s2 at 4500 m below sea level to 7.3218 m/s2 at 100,000 m above sea level. However, at altitudes up to 30,000 m, the variation
of g from the sea level value of 9.807 m/s2 is less than 1 percent. Therefore, for most practical purposes, the gravitational acceleration can be assumed to be constant at 9.81 m/s2. It is interesting to note that at locations below sea level, the value of g increases with distance from the sea level, reaches a maximum at about 4500 m, and then starts decreasing. (What do you think the value of g is at the center of the earth?)
The primary cause of confusion between mass and weight is that mass is usually measured indirectly by measuring the gravity force it exerts. This approach also assumes that the forces exerted by other effects such as air buoyancy and fluid motion are negligible. This is like measuring the distance to a star by measuring its red shift, or measuring the altitude of an airplane by measuring barometric pressure. Both of these are also indirect measurements. The correct direct way of measuring mass is to compare it to a known mass. This is cumbersome, however, and it is mostly used for calibration and mea- suring precious metals.
Work, which is a form of energy, can simply be defined as force times distance; therefore, it has the unit “newton-meter (N · m),” which is called a joule (J). That is,
A more common unit for energy in SI is the kilojoule (1 kJ = 103 J). In the English system, the energy unit is the Btu (British thermal unit), which is defined as the energy required to raise the temperature of 1 lbm of water at 68°F by 1°F. In the metric system, the amount of energy needed to raise the temperature of 1 g of water at 15°C by 1°C is defined as 1 calorie (cal), and 1 cal = 4.1868 J. The magnitudes of the kilojoule and Btu are almost identi- cal (1 Btu = 1.055 kJ).
Dimensional Homogeneity
We all know from grade school that apples and oranges do not add. But we somehow manage to do it (by mistake, of course). In engineering, all equations must be dimensionally homogeneous. That is, every term in an equation must have the same unit (Fig. 1–14). If, at some stage of an analysis, we find ourselves in a position to add two quantities that have different units, it is a clear indication that we have made an error at an earlier stage. So checking dimensions can serve as a valuable tool to spot errors.
The student should keep in mind that a formula that is not dimensionally homogeneous is definitely wrong, but a dimensionally homogeneous formula is not necessarily right.