Pipeline scaling parameters
Introduction
Although reliable models are now well established for single phase flow, no such relationships are available for gas–solid flows. The use of mathematical models is very limited, both in terms of the range of conveying conditions over which they can be applied and the range of materials for which they are applicable. Test data, therefore, is probably more widely used for system design and, if a system has to be designed for a material for which no previous experience exists, it is usual to carry out tests with the material in order to obtain the necessary data. Most companies in the business of manufacturing and sell- ing pneumatic conveying systems have test facilities for this very purpose.
As it is rarely practicable to convey a material through a test pipeline of the exact geometry as the one to be built, it is usually necessary to scale the conveying charac- teristics obtained from a test pipeline to that required. If a number of design alterna- tives are to be considered, additional scaling will be necessary, for the conveying of a material through a range of pipelines of different bore will be very expensive and time consuming. Scaling in terms of pipeline geometry needs to be carried out with respect to conveying distance, pipeline bore, pipeline orientation, and the number of bends in the pipeline. Pipeline material, bend geometry, and stepped pipelines are other important parameters that also need to be considered.
The design of the pipeline is probably one of the first tasks to be undertaken in pneu- matic conveying system design. The conveying distance and material flow rate for the plant are usually specified, and so it is necessary to determine the pipeline bore and the air supply pressure required. The starting point in this process is generally test data or some previous experience with the particular material to be conveyed. If the conveying characteristics are available for a material in a known pipeline they can be scaled, for the same material, to another pipeline, with a reasonable degree of accuracy.
Scaling requirements
The main requirements of scaling are that dynamic similarity should be maintained and that the scaling should remain within established flow regimes.
Conveying air velocity
If, for a given material, conveying data relating to one pipeline is to be scaled to that for another pipeline, it is essential that conveying conditions, in terms of air velocities,
should be the same for the two situations. This means that scaling must be carried out for data points having the same conveying line pressure drop and air mass flow rate. If scaling is in terms of pipeline bore, the air mass flow rate must be in proportion to the pipe section area, or (diameter)2 for a given conveying line pressure drop, to maintain similar air velocities.
Solids loading ratio
The data available from previous experience, or from conveying trials undertaken, should not be extended to higher values of solids loading ratio.
Conveying distance
To illustrate the scaling procedure with respect to conveying distance, the conveying characteristics for two materials with very different conveying capabilities are used. One is ordinary Portland cement, which is capable of being conveyed in dense phase and at low velocity, if the conveying line pressure gradient is high enough. The other is potassium sulphate, which can only be conveyed in dilute phase suspension flow, in a conventional conveying system, even if a high air supply pressure is used.
Both of these materials were conveyed through pipeline no. 6, which is 95 m long, of 81 mm bore and incorporates nine 90° bends having a D/d ratio of 16:1 (Figure 12.24). The conveying characteristics of the two materials were presented in Figure 12.23 and are reproduced here in Figure 14.1 for reference.
In each case conveying was carried out with line pressure drop values of up to about
for the potassium sulphate was only ten. This illustrates quite clearly the significant difference in conveying potential that can exist between different materials. With a con- veying line pressure drop of 3 bar the cement could be conveyed at about 40 tonne/h and with only 0.085 kg/s of air, whereas the flow rate of the potassium sulphate was only 12 tonne/h and required 0.35 kg/s of air.
Minimum conveying air velocity
The relationship between the minimum conveying air velocity and the solids loading ratio at which the materials can be conveyed is presented in Figure 14.2. For the dilute phase conveying of the cement a minimum conveying air velocity of 11 m/s is required, but for the potassium sulphate it is about 14 m/s. At higher solids loading ratios the minimum conveying air velocity for the cement decreases until it is about 3 m/s, at a solids loading ratio of about 70. For the potassium sulphate the minimum conveying air velocity remains at 14 m/s. This is because conveying at a solids loading ratio greater than about 12 is not possible, even with much higher air supply pressures, in a conventional conveying system.
Scaling
To illustrate the influence of distance fully, the entire conveying characteristics for the two materials are first scaled to a conveying distance of 150 m and then to 200 m.
Empty line pressure drop
The pressure drop, Dp, for the flow of air through a pipeline of a given diameter, d, and length, L, can be determined from Darcy’s Equation, presented in Equation (10.2). This is reproduced here for reference:
With an increase in distance there will be a similar increase in pressure drop, both for the air in the empty line and for the conveying of the material. The increase in pressure drop for the empty line increases approximately in proportion to the increase in length, as will be seen from Equation (14.1). Data for the empty lines being considered is given in Figure 14.3.
Figure 14.3 shows the variation of pressure drop with air flow rate for the 95 m long pipeline of 81 mm bore, and for the 150 m and 200 m long pipelines of the same bore. For the scale up of the conveying characteristics in respect of distance, the change in datum for the empty line will have to be taken into account. If the air supply pressure remains the same, for an increase in conveying distance, an increase in the air only pres- sure drop value will mean a corresponding reduction in the pressure drop available for the conveying of the material.
Scaling model
Scale up of material flow rate with respect to conveying distance can be carried out with a reasonable degree of accuracy, if the extrapolation is not too great, on the basis of a reciprocal law:
For a constant conveying air flow rate and pressure drop due to the conveyed material.
Where m· , material flow rate; L , equivalent length of pipeline; subscripts 1 and 2 relate to the test pipeline and the plant pipeline.
Conveying distance is expressed in terms of an equivalent length of the total pipeline. This comprises the three main elements of the pipeline routing or geometry. One is the length of the horizontal sections of pipeline, the second is the length of vertically up sections of the pipeline, and the third relates to the bends in the pipeline. Horizontal pipeline is taken as the reference. To this is added the equivalent length of straight horizontal pipeline represented by vertical sections of pipeline, and the equiva- lent length for all the bends in the pipeline.
For the purpose of illustrating the influence of conveying distance additional pipeline lengths of 150 and 200 m are used. The equivalent length of vertical pipeline and bends are considered in later sections of this chapter. For this exercise equivalent lengths have been taken as the length of horizontal pipeline, purely for simplicity in terms of illustration, in advance of considering vertical elements of pipeline and bends.
The working form of this scaling model is:
Scaling procedure
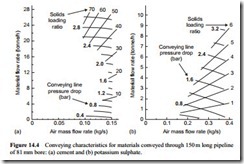
For the scaling of the two sets of data presented in Figure 14.1, conveyed over a dis- tance of 95 m, to a distance of 150 m, the datum pressure drop for the air only should first be changed throughout by the values given in Figure 14.3. Material flow rates, for given air mass flow rates and conveying line pressure drops, are then scaled in the ratio of Le1/Le2. The results of this are presented in Figure 14.4.
It can be seen from Figure 14.4a that the maximum value of cement flow rate has reduced from about 40 tonne/h over 95 m, to about 26 tonne/h over 150 m, for the same 3.0 bar pressure drop. This represents a 35 per cent reduction in cement flow rate, but this would be expected from Equation (14.4). A particularly important point to note is that the maximum value of solids loading ratio has dropped from just over 120 to about 70, which represents a 42 per cent reduction.
The reduction in solids loading ratio is clearly due to the decrease in cement flow rate. This increased reduction in solids loading ratio, however, is due to the fact that a higher value of conveying line inlet air velocity is required as a result of the lower value of solids loading ratio at which the cement is conveyed.
Solids loading ratio has a significant effect on the value of minimum conveying air velocity, as was shown in Figure 14.2. It is the need for a slightly higher conveying line inlet air velocity, and hence a higher air mass flow rate, that has caused the increased reduction in solids loading ratio.
Cement conveying limits
Conveying distance will have a significant effect on this particular relationship but so also does pressure since it is primarily a function of pressure gradient. This means that the limit of conveying, in terms of air mass flow rate, has to be changed for each pres- sure drop line according to the new conditions. The appropriate model for conveying line inlet air velocity was presented with Equation (9.20) and is reproduced here as Equation (14.5) for reference:
By using Equation (14.5), in conjunction with the relationship presented in Figure 14.2 for the cement, the locus of the conveying limit in Figure 14.4a can be established. It is a ‘trial and error’ solution, but with Equation (14.5) programmed into a calculator it should only take a matter of seconds to establish the value of minimum air mass flow rate for each conveying line pressure drop curve, and so determine the new boundary for the limit of conveying.
Potassium sulphate conveying limit
In the case of the potassium sulphate both the material flow rate and the solids loading ratio have reduced in proportion to the ratio of distances. This is because there is no change in value of the minimum velocity for the material, as will be seen from Figure 14.2, and hence the air flow rates required remain unchanged. The conveying characteristics for the potassium sulphate over 150 m are essentially geometrically similar to those for the material over 95 m. The only difference is due to the change in air only pressure drop values and not to a change in conveying limits.
Scaling to longer distances
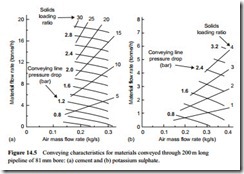
The results of the scaling of the conveying characteristics for the two materials to a distance of 200 m are presented in Figure 14.5.
For the cement in Figure 14.5a a very significant change has occurred, with an increase of the air flow rate axis required to accommodate the data. Compared with this same material conveyed over only about half the distance in Figure 14.1a, the maximum cement flow rate has been reduced from about 40 to 19 tonne/h. This, as explained above, is to be expected from Equation (14.4) and the increase in air only pressure drop. It is the reduction of the maximum value of solids loading ratio from 120 to 30 that has an over-riding effect on performance.
Dense phase conveying limit
It will be seen from Figure 14.5a that if the maximum flow rate capability of the compressor was limited to about 0.115 kg/s (200 ft3/min), it would not be possible to use the compressor at all for conveying over a distance of 200 m, not even by restricting the pressure and using it for dilute phase conveying of the cement. From Equation (14.5) it will be seen that for a conveying line pressure drop of 0.8 bar and temperature of 20°C the conveying line inlet air velocity is only 10.6 m/s.
The relationship between inlet air velocity and solids loading ratio, as shown in Figure 14.2, is extremely important for materials capable of being conveyed in dense phase. Although the change in cement flow rate, with increase in distance, is as predicted by the model, the reduction in solids loading ratio is significantly more. A further increase in distance would result in this reducing to a point at which the cement could only be con- veyed in dilute phase.
With a further increase in distance the boundary limit to conveying would be little different from those for the potassium sulphate, although the flow rate would remain at a slightly higher value. Dense phase conveying requires a high pressure gradient which is typically about 20 mbar/m for horizontal conveying at a solids loading ratio of about 100 (see Figure 1.1). Pressure gradient is simply the available pressure divided by conveying distance. Dense phase conveying, therefore, is possible, even with neg- ative pressure systems, provided that the distance is short. For conveying over longer distances, higher pressures will be required, but there is a limit.
Iterative process
In scaling the conveying characteristics for the cement to longer distances, the upper part of the conveying characteristics become unavailable for scaling, since this is the area of maximum solids loading ratio and lowest velocity. A reduction in cement flow rate will automatically reduce the solids loading ratio by the same amount, for a given air flow rate and pressure drop, and this reduction in solids loading ratio will necessi- tate a correspondingly higher value of inlet air velocity. This means that a higher air flow rate will be required, which in turn means a further lowering of the solids loading ratio, as discussed above.
Over an even longer distance, therefore, it is clear that the cement will be restricted to dilute phase conveying, and if a conveying line pressure drop of 3.0 bar should need to be utilized, an air flow rate much higher than 0.115 kg/s would be required. In this case it is likely that the conveying line exit air velocity would be in excess of 50 m/s for a single bore pipeline. Great care must be taken, therefore, if a change in distance is needed for a material which is capable of being conveyed in dense phase. Air requirements for con- veying a material must be based on the longest distance, and a reduction in air flow rate should ideally be made to achieve optimum conveying conditions over shorter distances.
For the potassium sulphate in Figure 14.5b the conveying characteristics have reduced almost geometrically, with a halving of both material flow rate and solids load- ing ratio, and no change in air requirements. In this case an iterative process of deter- mining the minimum conveying limits is not necessary because there is no change in minimum conveying air velocity with respect to solids loading ratio for this material.
Note
It should be pointed out that the influence of bends in the pipeline has been taken into account in these examples. The number of bends has been scaled in proportion and so the conveying characteristics for the cement conveyed over 200 m includes approximately 19 bends. The number of bends in a pipeline can have a major influence on the conveying characteristics, as will be shown later, and the large number in this case has had a significant effect on the rapid transition from dense phase conveying, over 95 m, to almost dilute phase conveying, over 200 m, for the cement. The transition does not generally happen as quickly as this, since the example is a little artificial, but it is nevertheless illustrative of the process which is the main point of the exercise.