THE FIRST LAW OF THERMODYNAMICS:SOME STEADY-FLOW ENGINEERING DEVICES

SOME STEADY-FLOW ENGINEERING DEVICES

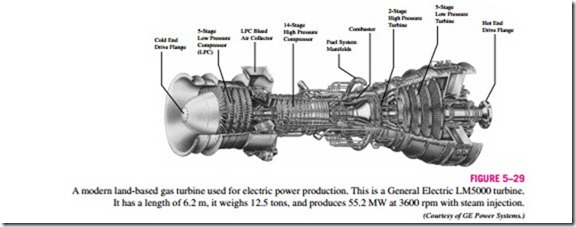
Many engineering devices operate essentially under the same conditions for long periods of time. The components of a steam power plant (turbines, com- pressors, heat exchangers, and pumps), for example, operate nonstop for months before the system is shut down for maintenance (Fig. 5–29). There- fore, these devices can be conveniently analyzed as steady-flow devices.

In this section, some common steady-flow devices are described, and the thermodynamic aspects of the flow through them are analyzed. The conservation of mass and the conservation of energy principles for these devices are illustrated with examples.

1 Nozzles and Diffusers

Nozzles and diffusers are commonly utilized in jet engines, rockets, spacecraft, and even garden hoses. A nozzle is a device that increases the velocity

of a fluid at the expense of pressure. A diffuser is a device that increases the pressure of a fluid by slowing it down. That is, nozzles and diffusers perform opposite tasks. The cross-sectional area of a nozzle decreases in the flow direction for subsonic flows and increases for supersonic flows. The reverse istrue for diffusers.

The rate of heat transfer between the fluid flowing through a nozzle or a diffuser and the surroundings is usually very small ( · = 0) since the fluid has high velocities, and thus it does not spend enough time in the device for any significant heat transfer to take place. Nozzles and diffusers typically involve no work ( · = 0) and any change in potential energy is negligible (Dpe – 0).

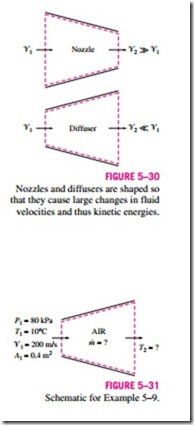
But nozzles and diffusers usually involve very high velocities, and as a fluid passes through a nozzle or diffuser, it experiences large changes in its velocity (Fig. 5–30). Therefore, the kinetic energy changes must be accounted for in analyzing the flow through these devices

2 Turbines and Compressors

In steam, gas, or hydroelectric power plants, the device that drives the electric generator is the turbine. As the fluid passes through the turbine, work is done against the blades, which are attached to the shaft. As a result, the shaft rotates, and the turbine produces work. The work done in a turbine is positive since it is done by the fluid.

Compressors, as well as pumps and fans, are devices used to increase the pressure of a fluid. Work is supplied to these devices from an external source through a rotating shaft. Therefore, compressors involve work inputs. Even though these three devices function similarly, they do differ in the tasks they perform. A fan increases the pressure of a gas slightly and is mainly used to mobilize a gas. A compressor is capable of compressing the gas to very high pressures. Pumps work very much like compressors except that they handle liquids instead of gases.

Note that turbines produce power output whereas compressors, pumps, and fans require power input. Heat transfer from turbines is usually negligible for compressors unless there is intentional cooling. Potential energy changes are negligible for all of these devices (�pe � 0). The velocities involved in these devices, with the exception of turbines and fans, are usually too low to cause any significant change in the kinetic energy (�ke � 0). The fluid velocities encountered in most turbines are very high, and the fluid experiences a significant change in its kinetic energy. However, this change is usually very small relative to the change in enthalpy, and thus it is often disregarded.

3 Throttling Valves

Throttling valves are any kind of flow-restricting devices that cause a significant pressure drop in the fluid. Some familiar examples are ordinary adjustable valves, capillary tubes, and porous plugs (Fig. 5–35). Unlike turbines, they produce a pressure drop without involving any work. The pressure drop in the fluid is often accompanied by a large drop in temperature, and for that reason throttling devices are commonly used in refrigeration and air-conditioning applications. The magnitude of the temperature drop (or, sometimes, the temperature rise) during a throttling process is governed by a property called the Joule-Thomson coefficient.

Throttling valves are usually small devices, and the flow through them may be assumed to be adiabatic (q � 0) since there is neither sufficient time nor large enough area for any effective heat transfer to take place. Also, there is no work done (w = 0), and the change in potential energy, if any, is very small (�pe � 0). Even though the exit velocity is often considerably higher than the inlet velocity, in many cases, the increase in kinetic energy is insignificant (�ke � 0). Then the conservation of energy equation for this single-stream steady-flow device reduces to

That is, enthalpy values at the inlet and exit of a throttling valve are the same. For this reason, a throttling valve is sometimes called an isenthalpic device. Note, however, that for throttling devices with large exposed surface areas such as capillary tubes, heat transfer may be significant.

To gain some insight into how throttling affects fluid properties, let us ex- press Eq. 5–22 as follows:

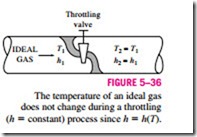
Thus the final outcome of a throttling process depends on which of the two quantities increases during the process. If the flow energy increases during the process (P2u2 > P1u1), it can do so at the expense of the internal energy. As a result, internal energy decreases, which is usually accompanied by a drop in temperature. If the product Pu decreases, the internal energy and the temperature of a fluid will increase during a throttling process. In the case of an ideal gas, h = h(T ), and thus the temperature has to remain constant during a throttling process (Fig. 5–36).

4a Mixing Chambers

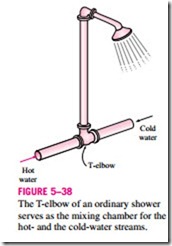
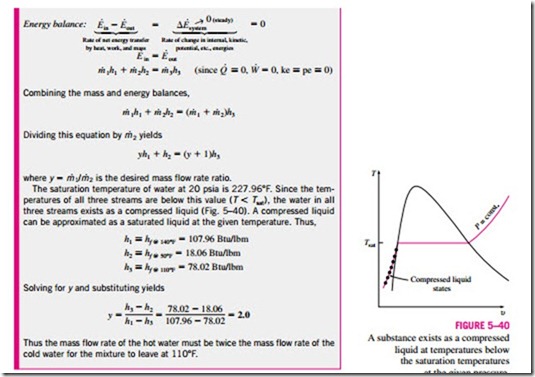
In engineering applications, mixing two streams of fluids is not a rare occurrence. The section where the mixing process takes place is commonly referred to as a mixing chamber. The mixing chamber does not have to be a distinct “chamber.’’ An ordinary T-elbow or a Y-elbow in a shower, for example, serves as the mixing chamber for the cold- and hot-water streams (Fig. 5–38). The conservation of mass principle for a mixing chamber requires that the sum of the incoming mass flow rates equal the mass flow rate of the outgoing mixture.

Mixing chambers are usually well insulated (q � 0) and do not involve any kind of work (w = 0). Also, the kinetic and potential energies of the fluid streams are usually negligible (ke � 0, pe � 0). Then all there is left in the energy balance is the total energies of the incoming streams and the outgoing mixture. The conservation of energy principle requires that these two equal each other. Therefore, the conservation of energy equation becomes analogous to the conservation of mass equation for this case.

4b Heat Exchangers

As the name implies, heat exchangers are devices where two moving fluid streams exchange heat without mixing. Heat exchangers are widely used in various industries, and they come in various designs.

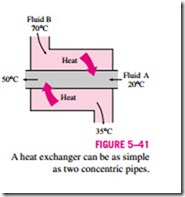
The simplest form of a heat exchanger is a double-tube (also called tube- and-shell) heat exchanger, shown in Fig. 5–41. It is composed of two concentric pipes of different diameters. One fluid flows in the inner pipe, and the other in the annular space between the two pipes. Heat is transferred from the hot fluid to the cold one through the wall separating them. Sometimes the inner tube makes a couple of turns inside the shell to increase the heat trans- fer area, and thus the rate of heat transfer. The mixing chambers discussed earlier are sometimes classified as direct-contact heat exchangers.

The conservation of mass principle for a heat exchanger in steady operation requires that the sum of the inbound mass flow rates equal the sum of the out- bound mass flow rates. This principle can also be expressed as follows: Under steady operation, the mass flow rate of each fluid stream flowing through a heat exchanger remains constant.

Heat exchangers typically involve no work interactions (w = 0) and negli- gible kinetic and potential energy changes (�ke � 0, �pe � 0) for each fluid

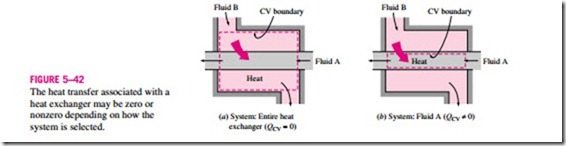
stream. The heat transfer rate associated with heat exchangers depends on how the control volume is selected. Heat exchangers are intended for heat transfer between two fluids within the device, and the outer shell is usually well insulated to prevent any heat loss to the surrounding medium. ·

When the entire heat exchanger is selected as the control volume, Q becomes zero, since the boundary for this case lies just beneath the insulation and little or no heat crosses the boundary (Fig. 5–42). If, however, only one of the fluids is selected as the control volume, then heat will cross this boundary as it flows from one fluid to the other and Q will not be zero. In fact, Q in this case will be the rate of heat transfer between the two fluids.

5 Pipe and Duct Flow

The transport of liquids or gases in pipes and ducts is of great importance in many engineering applications. Flow through a pipe or a duct usually satisfies the steady-flow conditions and thus can be analyzed as a steady-flow process. This, of course, excludes the transient start-up and shut-down periods. The control volume can be selected to coincide with the interior surfaces of the portion of the pipe or the duct that we are interested in analyzing.

Under normal operating conditions, the amount of heat gained or lost by the fluid may be very significant, particularly if the pipe or duct is long (Fig. 5–45). Sometimes heat transfer is desirable and is the sole purpose of the flow. Water flow through the pipes in the furnace of a power plant, the flow of refrigerant in a freezer, and the flow in heat exchangers are some examples of this case. At other times, heat transfer is undesirable, and the pipes or ducts are insulated to prevent any heat loss or gain, particularly when the temperature difference between the flowing fluid and the surroundings is large. Heat trans- fer in this case is negligible.

If the control volume involves a heating section (electric wires), a fan, or a pump (shaft), the work interactions should be considered (Fig. 5–46). Of these, fan work is usually small and often neglected in energy analysis.

The velocities involved in pipe and duct flow are relatively low, and the kinetic energy changes are usually insignificant. This is particularly true when the pipe or duct diameter is constant and the heating effects are negligible. Kinetic energy changes may be significant, however, for gas flow in ducts with variable cross-sectional areas especially when the compressibility effects are significant. The potential energy term may also be significant when the fluid undergoes a considerable elevation change as it flows in a pipe or duct.