Material property influences
Introduction
In the previous chapter conveying characteristics were presented for a wide range of materials, both to illustrate the differences that can exist between materials and to provide reference data on materials. From the large number of materials considered certain material property influences were beginning to emerge with respect to identifying the potential of materials for low velocity dense phase conveying, but there were no clear guidelines.
In this chapter a review of possible material classifications and correlations are presented. These will show what has been done by way of trying to identify material prop- erties that might provide a little more guidance on identifying the potential capability of a new and untried material for dense phase conveying, and the possible mode of flow that might be achieved with the material.
A particular problem in pneumatic conveying is that materials are often identified simply by means of a name, such as soda ash and fly ash. This is never sufficient for pneumatic conveying purposes. Many materials are available in a wide variety of forms and grades, such as sugar, with granulated, caster and icing, and the performance and capability of all three of these different ‘grades’ will be very different. This is apart from considering the range of brown sugars, such as Demerara, that tend to be very cohesive.
With friable materials pneumatic conveying of the material can also change the grade of the material and this can have totally unexpected consequences on the performance of the conveying system. These effects, therefore, are illustrated with a number of materials and these changes are also related to material performance correlations.
Conveying modes
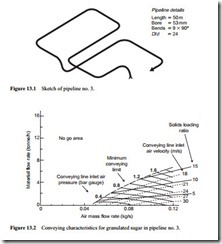
To set the scene here a recap on the three main modes of conveying is presented. For this purpose three materials conveyed through pipeline no. 3 (Figure 12.12) are used as this will allow a direct visual comparison of performance. A sketch of the pipeline is given in Figure 13.1 for reference here.
Dilute phase non-suspension flow
Granulated sugar has been selected as being representative of materials conveyed in dilute phase and the conveying characteristics are presented in Figure 13.2. These
were presented earlier in Figure 12.11b. In Figure 13.2 they are shown with the inclusion of lines of constant conveying line inlet air velocity, since this is a critical parameter in distinguishing between dilute and dense phase flows.
Virtually any material, as has been mentioned before, can be conveyed in dilute phase. This also includes materials that are capable of being conveyed in dense phase. If the pressure gradient available for conveying a material is low either, because the pipeline is long or the air supply pressure is low, it will only be possible to convey materials that have dense phase conveying potential in dilute phase suspension flow. This point was illustrated in Figure 1.1.
The form of the conveying characteristics shown in Figure 13.2 is typical of all materials conveyed in dilute phase. The minimum value of conveying air velocity will be of the order of 10–12 m/s for fine powders, being closer to 10 m/s for ground materials such as flour and cement because of the particle shape. It will be in the region of 13–16 m/s for fine granular materials, being closer to 13 m/s if the material has a wide particle size distribution. That for granulated sugar was about 16 m/s. For materials that can only be conveyed in dilute phase suspension flow there is little change in the value of minimum conveying air velocity with the concentration of the material conveyed, or its solids loading ratio.
The conveying limit identified in Figure 13.2 has a positive slope as shown due to entirely the fact that air is compressible and the minimum value of conveying air velocity remains essentially constant. As the conveying line inlet air pressure, and hence the air supply pressure, increases more air is required to maintain the same velocity. It will be seen that the lines of constant conveying line inlet air velocity superimposed have a similar slope, since the minimum conveying limit is represented by a conveying line inlet air velocity of 16 m/s. The equation governing this comes from Chapter 9 and is a re-arrangement of Equation (9.20) which relates to air:
where m.a is the air mass flow rate (kg/s); p1, conveying line inlet air pressure (kN/m2 abs); d, the pipeline bore (m); C1, the conveying line inlet air velocity (m/s) and T1, the con- veying line inlet air temperature (K).
Thus if the conveying line inlet air velocity remains constant, along with pipeline bore and temperature, the air flow rate must increase in proportion to the absolute pressure of the inlet air. On this plot lines of constant solids loading ratio are straight lines through the origin, as will be seen. As a consequence there is little scope for the material being conveyed at a higher value of solids loading ratio, even if a much higher air supply pressure was to be used, for the slope of the conveying limit curve (at 16 m/s) is only slightly steeper than that of the solids loading ratio line drawn at a value of 15.
Lines of constant conveying line inlet air velocity are also useful in terms of illustrating the adverse effect of velocity on conveying performance. Air flow rate on its own has no real meaning and is difficult to interpret, but conveying line inlet air vel- ocity is a fundamental design parameter for pneumatic conveying systems. Conveying air velocity has a very significant influence on conveying performance and in dilute phase conveying there is only a narrow band of operating values. As will be seen from Figure 13.2 for the granulate sugar, if the conveying line inlet air velocity is below 16 m/s nothing will be conveyed because the pipeline will block, and if it is greater than about 30 m/s almost nothing will be conveyed because all of the available energy is lost to friction. This is the velocity squared term in the pressure drop equations presented in Equations (1.4) and (10.2).