FORCES IN LIQUIDS:TRANSMISSION OF FORCE THROUGH LIQUIDS.

TRANSMISSION OF FORCE THROUGH LIQUIDS

When the end of a solid bar is struck, the main force of the blow is carried straight through the bar to the other end (Figure 2-7, view A). This happens because the bar is rigid. The direction of the blow almost entirely determines the direction of the trans mitted force. The more rigid the bar, the less force is lost inside the bar or transmitted outward at right angles to the direction of the blow.

When a force is applied to the end of a column of confined liquid (Figure 2-7, view B), it is transmitted straight through to the other end. It is also equal and undiminished in every direction throughout the column-forward, backward, and sideways-so that the containing vessel is literally filled with the added pressure.

So far we have explained the effects of atmospheric pressure on liquids and how external forces are distributed through liquids. Let us now focus our attention on forces generated by the weight of liquids themselves. To do this, we must first discuss density, specific gravity, and Pascal’s law.

PRESSURE AND FORCE IN HYDRAULIC SYSTEMS

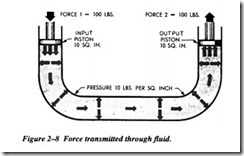
According to Pascal’s law, any force applied to a confined fluid is transmitted uni formly in all directions throughout the fluid regardless of the shape of the container. Consider the effect of this in the system shown in Figure 2-8.

If there is a resistance on the output piston and the input piston is pushed downward, a pressure is created through the fluid, which acts equally at right angles to surfaces in all parts of the container. If force 1 is 100 pounds and the area of the input piston is 10 square inches, then the pressure in the fluid is 10 psi.

Note: Fluid pressure cannot be created without resistance to flow. In this case, the equipment to which the output piston is attached provides resistance. The force of resistance acts against the top of the output piston. The pressure is created in the sys tem by the input piston pushing on the underside of the output piston with a force of 10 pounds per square inch.

In this case, the fluid column has a uniform cross-section, so the area of the output piston is the same as the area of the input piston, or 10 square inches. Therefore, the upward force on the output piston is 100 pounds and is equal to the force applied to the input piston. All that was accomplished in this system was to transmit the 100 pounds of force around the bend. However, this principle underlies practically all mechanical applications of hydraulics or fluid power.

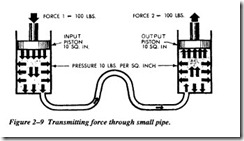
At this point, you should note that since Pascal’s law is independent of the shape of the container, it is not necessary that the tube connecting the two pistons have the same cross-sectional area as the pistons. A connection of any size, shape, or length will do, as long as an unobstructed passage is provided. Therefore, the system shown in Figure 2-9, with a relatively small, bent pipe connecting two cylinders, will act exactly the same as the system shown in Figure 2-8.

MULTIPLICATION OF FORCE

Unlike the preceding discussion, hydraulic systems can provide mechanical advan tage or a multiplication of input force. Figure 2-10 illustrates an example of an increase in output force. Assume that the area of the input piston is 2 square inches. With a resistant force on the output piston, a downward force of 20 pounds acting on the input piston will create a pressure of 20/2 or 10psi in the fluid. Although this force is much smaller than the force applied in Figures 2-8 and 2-9, the pressure is the same. This is because the force is applied to a smaller area.

This pressure of 10 psi acts on all parts of the fluid container, including the bottom of the output piston. The upward force on the output piston is 200 pounds (10 psi x pis ton area). In this case, the original force has been multiplied tenfold while using the same pressure in the fluid as before. In any system with these dimensions, the ratio of output force to input force is always 10 to 1, regardless of the applied force. For example, if the applied force of the input piston is 50 pounds, the pressure in the sys tem will be 25 psi. This will support a resistant force of 500 pounds on the output pis ton. The system works the same in reverse.

If we change the applied force and place a 200-pound force on the output piston (Figure 2-11), making it the input piston, the output force on the input piston will be one-tenth the input force, or 20 pounds. Therefore, if two pistons are used in a fluid power system, the force acting on each piston is directly proportional to its area, and the magnitude of each force is the product of the pressure and the area of each piston.

DIFFERENTIAL AREAS

Figure 2-11 is a simple example of differential pressure. The figure illustrates a single piston with a surface area of 6 square inches, attached to a piston rod with an area of 2 square inches. Without any external force applied to the end of the piston rod, an equal force, 20 psig, applied to both sides of the piston, will cause the piston to move to the right. This motion is the result of differential forces. Even though the input force, 20 psig, is applied to both sides of the piston, the difference in area, 6 in2 on the left face,

and 2 in2 on the right face, will cause the piston to move. The opposed faces of the pis ton behave like two pistons acting against each other. The area of one face is the full cross-sectional area of the cylinder or 6 square inches, while the area of the opposing face is the area of the piston minus the area of the piston rod, or 2 square inches. This leaves an effective area of 4 square inches on the piston rod side of the piston.

The force acting on the left side of the piston is equal to 20 psi x 6 square inches or 120 pounds. The opposing force generated by the right side of the piston is 20 psi x 4 square inches or 80 pounds. Therefore, there is a net unbalanced force of 40 pounds (120- 80) acting on the right, and the piston will move in that direction.

VOLUME AND DISTANCE FACTORS

You have learned that if a force is applied to a system and the cross-sectional areas of the input and output are equal, the force on the input piston will support an equal resistant force on the output piston. The pressure of the liquid at this point is equal to the force applied to the input piston divided by the piston’s area. Let us now look at what happens when a force greater than the resistance is applied to the input piston.

In the system illustrated in Figure 2-8, assume that the resistant force on the output piston is 100 pounds. If a force slightly greater than 100 pounds is applied to the input piston, the pressure in the system will be slightly greater than 10 psi. This increase in pressure will overcome the resistant force on the output piston. If the input piston is forced downward 1 inch, the movement displaces 10 cubic inches of fluid. The fluid must go somewhere. Since the system is closed and the fluid is practically incompressible, the fluid will move the right side of the system. Because the output piston also has a cross-sectional area of 10 square inches, it will move upward 1 inch to accommodate the 10 cubic inches of fluid. You may generalize this by saying that if two pistons in a closed system have equal cross-sectional areas and one piston is pushed and moved, the other piston will move the same distance in the opposite direc tion. This is because a decrease in volume in one part of the system is balanced by an equal increase in volume in another part of the system.

Apply this reasoning to the system in Figure 2-9. If the input piston is pushed down a distance of 1 inch, the volume in the left cylinder will decrease by 2 cubic inches. At the same time, the volume in the right cylinder will increase by 2 cubic inches. Since the diameter of the right cylinder cannot change, the piston must move upward to allow the volume to increase. The piston will move a distance equal to the volume increase divided by the surface area of the piston. In this example, the piston will move one-tenth of an inch (2 cubic inches/20 square inches).

This leads to the second basic rule for fluid power systems that contain two pistons: The distances the pistons move are inversely proportional to their areas. Or, more simply, if one piston is smaller than the other, the smaller piston must move a greater distance than the larger piston any time the pistons move.