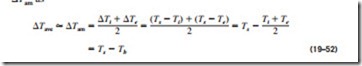GENERAL THERMAL ANALYSIS
You will recall that in the absence of any work interactions (such as electric resistance heating), the conservation of energy equation for the steady flow of a fluid in a tube can be expressed as (Fig. 19–23) .
where Ti and Te are the·mean fluid temperatures at the inlet and exit of the tube, respectively, and Q is the rate of heat transfer to or from the fluid. Note that the temperature of a fluid flowing in a tube remains constant in the absence of any energy interactions through the wall of the tube.
The thermal conditions at the surface can usually be approximated with reasonable accuracy to be constant surface temperature (Ts = constant) or constant surface heat flux ( · = constant). For example, the constant surface temperature condition is realized when a phase change process such as boiling or condensation occurs at the outer surface of a tube. The constant surface heat flux condition is realized when the tube is subjected to radiation or electric resistance heating uniformly from all directions.
Surface heat flux is expressed as
where hx is the local heat transfer coefficient and Ts and Tm are the surface and the mean fluid temperatures at that location. Note that the mean fluid temperature Tm of a fluid flowing in a tube must change during heating or cooling. Therefore, when hx = h = constant, the surface temperature Ts must change when qs = constant, and the surface heat flux qs must change when Ts = constant. Thus we may have either T = constant or · = constant at the surface of a tube, but not both. Next we consider convection heat transfer for these two common cases.
Constant Surface Heat Flux (qs = constant)
In the case of qs = constant, the rate of heat transfer can also be expressed as
Note that the mean fluid temperature increases linearly in the flow direction in the case of constant surface heat flux, since the surface area increases linearly
in the flow direction (As is equal to the perimeter, which is constant, times the tube length).
The surface temperature in the case of constant surface heat flux qs can be determined from
where h is the average convection heat transfer coefficient, As is the heat trans- fer surface area (it is equal to pDL for a circular pipe of length L), and !JTave is some appropriate average temperature difference between the fluid and the surface. Below we discuss two suitable ways of expressing !JTave.
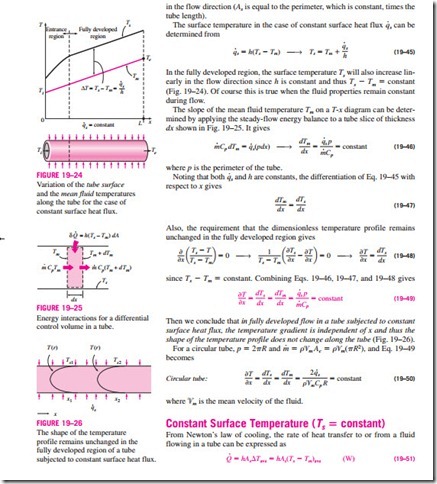
In the constant surface temperature (Ts = constant) case, !JTave can be expressed approximately by the arithmetic mean temperature difference
where Tb = (Ti + Te)/2 is the bulk mean fluid temperature, which is the arithmetic average of the mean fluid temperatures at the inlet and the exit of the tube.
Note that the arithmetic mean temperature difference !JTam is simply the average of the temperature differences between the surface and the fluid at the inlet and the exit of the tube. Inherent in this definition is the assumption that the mean fluid temperature varies linearly along the tube, which is hardly ever the case when Ts = constant. This simple approximation often gives accept- able results, but not always. Therefore, we need a better way to evaluate !JTave. Consider the heating of a fluid in a tube of constant cross section whose inner surface is maintained at a constant temperature of Ts. We know that the mean temperature of the fluid Tm will increase in the flow direction as a result of heat transfer. The energy balance on a differential control volume shown in Fig. 19–25 gives
That is, the increase in the energy of the fluid (represented by an increase in its mean temperature by dTm) is equal to the heat transferred to the fluid from the tube surface by convection. Noting that the differential surface area is dAs = pdx, where p is the perimeter of the tube, and that dTm = –d(Ts – Tm), since Ts is constant, the last relation can be rearranged as
where As = pL is the surface area of the tube and h is the constant average convection heat transfer coefficient. Taking the exponential of both sides and solving for Te gives the following relation which is very useful for the determination of the mean fluid temperature at the tube exit:
This relation can also be used to determine the mean fluid temperature Tm(x) at any x by replacing As = pL by px.
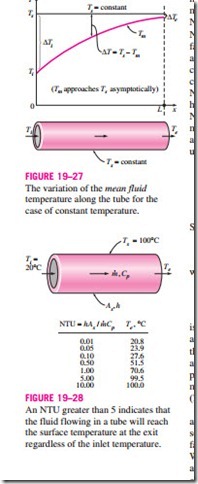
Note that the temperature difference between the fluid and the surface de- cays exponentially in the flow direction, and the rate of decay depends on the mensionless parameter is called the number of transfer units, denoted by NTU, and is a measure of the effectiveness of the heat transfer systems. For NTU > 5, the exit temperature of the fluid becomes almost equal to the surface temperature, Te = Ts (Fig. 19–28). Noting that the fluid temperature can approach the surface temperature but cannot cross it, an NTU of about 5 indi- cates that the limit is reached for heat transfer, and the heat transfer will not in- crease no matter how much we extend the length of the tube. A small value of NTU, on the other hand, indicates more opportunities for heat transfer, and the heat transfer will continue increasing as the tube length is increased. A large NTU and thus a large heat transfer surface area (which means a large tube) may be desirable from a heat transfer point of view, but it may be unacceptable from an economic point of view. The selection of heat transfer equipment usually reflects a compromise between heat transfer performance and cost.
is the logarithmic mean temperature difference. Note that !JTi = Ts – Ti and !JTe = Ts – Te are the temperature differences between the surface and the fluid at the inlet and the exit of the tube, respectively. This !JTln relation appears to be prone to misuse, but it is practically fail-safe, since using Ti in place of Te and vice versa in the numerator and/or the denominator will, at most, affect the sign, not the magnitude. Also, it can be used for both heating (Ts > Ti and Te) and cooling (Ts < Ti and Te) of a fluid in a tube.
An NTU greater than 5 indicates that the fluid flowing in a tube will reach the surface temperature at the exit regardless of the inlet temperature.
The logarithmic mean temperature difference !JTln is obtained by tracing the actual temperature profile of the fluid along the tube, and is an exact representation of the average temperature difference between the fluid and the sur- face. It truly reflects the exponential decay of the local temperature difference. When !JTe differs from !JTi by no more than 40 percent, the error in using the arithmetic mean temperature difference is less than 1 percent. But the error in- creases to undesirable levels when !JTe differs from !JTi by greater amounts. Therefore, we should always use the logarithmic mean temperature difference when determining the convection heat transfer in a tube whose surface is maintained at a constant temperature Ts.