Design procedures
Introduction
It is essential however that the available data relates to the same grade of material for which the new plant design is required. It is also essential that the data is available to slightly higher values of solids loading ratio and to slightly lower values of conveying line inlet air velocity, than are contemplated for the new design. Existing data should never be scaled beyond known conveying boundaries. In cases where no previous experience of the material or the range of conveying conditions required is available, then conveying trials are usually carried out in order to obtain the necessary test data for system design purposes.
A set of logic diagrams are presented and these can be used for the purpose of both designing a new conveying system and for checking the capability of an existing system, using both mathematical models and test data.
The use of equations in system design
The design of pneumatic conveying systems using mathematical models is generally the preferred method. There are, however, a limited number of reliable equations avail- able at present.
Logic diagram for system design
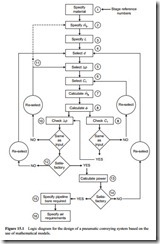
A logic diagram for the design of a pneumatic conveying system based on the use of mathematical models is presented in Figure 15.1. The procedure starts with the specifi- cation of the fixed parameters, goes through the necessary selection and calculation of conveying and system parameters to the final specification of the most suitable pipeline bore and air requirements. The numbers of the boxes in Figure 15.1 corresponds to the number of the sections in which the relevant calculation is discussed.
A bulk particulate material will be specified through a knowledge of some of all of the following parameters:
• Material name
• Bulk properties:
1. density,
2. particle size distribution,
3. free moisture,
4. permeability,
5. air retention.
• Particle properties:
1. density,
2. shape,
3. hardness,
4. friability.
Bulk densities, for example, are needed for the sizing of system components, such as rotary valves and blow tanks. Properties associated with drag, friction and shearing forces are desirable as these have an influence on the conveying potential for specified conveying conditions. Information on air retention and permeability would be useful as this relates to the potential mode of conveying and to the minimum conveying air velocity that can be employed. Particle hardness is important in terms of potential wear problems, and these are considered in detail in Chapter 23. Particle friability is simi- larly important in terms of material degradation and this is considered in Chapter 24.
For contractual reasons it would always be recommended that all parties involved should make a note of as many of the material properties as possible, for reference and identification purposes. These, of course, are the properties of the material upon which the design is based. Material property influences on conveying performance were considered at length in Chapter 13, where it was shown that a slight change in grade of a material can, with some materials, have a significant effect on the convey- ing capability of the material.
Specify mass flow rate of material required
This will generally be specified as a steady hourly rate, or a time averaged mean value. For continuously operating systems this value is the flow rate that needs to be specified. For batch operating systems the system will have to be designed to a higher value than this to take account of the fact that continuous conveying cannot be achieved, as discussed in relation to Figure 2.7. The ratio between the value to be specified for design purposes and the time averaged mean will depend upon the type of batch system to be used.
If the type of system required is known from the outset, then the appropriate value of material flow rate can be specified. If the investigation or survey is to cover a wide variety of pipeline bores, then a wide range of conveying line pressure drop values will result. The value of conveying line pressure drop may, to a certain extent, dictate the choice of system. The provisional feed-back loop to material flow rate specification,
therefore, is to take account of a change from continuous to batch operating systems which could occur within such an investigation.
The system design procedure outlined here relates essentially to the pipeline and specification of the air requirements to ensure that the material is conveyed at the specified flow rate. Due consideration will have to be given to the device used to feed the material into the conveying line, for this must also be capable of meeting the flow rate requirements. Feeder design and specification, however, can generally be considered in isolation from that of the pipeline system, and so is not included here. The same situation applies with regard to the design of systems for discharging the conveying line.
Specify conveying distance required
It will be required to specify the conveying distance, together with the routing and details of the pipeline. It is the actual distance that is of primary importance, but the ori- entation of the pipeline and the number of bends and their geometry are also important. Pipeline length has to be considered in terms of the individual lengths of horizontal, vertically up and vertically down sections. Bend geometry is considered in terms of the bend angle and the ratio of the bend diameter, D, to the pipe bore, d. The influence of pipeline length, orientation and bends were considered in detail in Chapter 14. Pipe- line bore is an entirely separate variable and is not considered at this stage.
Select pipeline bore
The diameter of the pipeline is one of the primary variables in terms of achieving a specified material flow rate through a pipeline. In combination with the conveying line pressure drop a wide range of pipeline bores will often meet the conveying require- ments, as illustrated with Figure 14.11. It is, therefore, necessary to select a value of pipeline bore, and in the first instance this may well be and estimated value or guess. If this proves to be unacceptable for some reason it will be necessary to re-select. This will be requested automatically by means of the various loops incorporated into the logic diagram. Subsequent values of pipeline bore, however, will be selected with the benefit of the initial estimate.
At this stage no provision is made for stepped pipelines. Should an increase in pipeline bore be required part way along its length, however, it could be designed in isolation. Such a design could be based on the required single pipeline bore, and steps could be evaluated as indicated in Section 9.4. A comparison of single and stepped bore pipelines was presented in Section 14.8 and it would be suggested that the math- ematical model being employed could be tested against that data, for the benefits achieved by stepping the pipeline are very material dependent.
Select conveying line pressure drop
In a similar manner to pipeline bore, it will be necessary to select a value of convey- ing line pressure drop. This may also be an estimated value or guess. If the selection is to be restricted to negative pressure or low pressure systems, however, the range will be limited automatically. Once again, if the value chosen proves to be unacceptable for some reason it will be necessary to re-select, and the necessary loop is incorporated for this purpose.
Select conveying line inlet air velocity
At the end of the design process two parameters will emerge. One is pipeline bore and the other is the air requirements, in terms of volumetric flow rate and pressure cap- ability. There is, therefore, a necessity for a conveying air velocity to be evaluated. Although the air velocity at free air conditions is the most convenient for this purpose, a major design parameter is that of the conveying air velocity at the material feed point into the pipeline. This is the conveying line inlet air velocity, C1.
The conveying line inlet air velocity is not a parameter whose value is estimated,and certainly not guessed. It must be selected and specified precisely. This is why, in Chapter 12, a multitude of values were given for the various materials considered so that a ‘feel’ for this critical design parameter would be obtained in terms of the differ- ent properties of the materials. That the value is dependent upon the type of material was illustrated with the compilation plots in Figures 12.4 and 12.15.
For dilute phase conveying the value of the minimum conveying air velocity, Cmin, will almost certainly be above 10 m/s. For cement it is about 10–11 m/s, fine fly ash 11–12 m/s, granular alumina 13–14 m/s and about 16 m/s for granulated sugar, the value depending mainly upon mean particle size, particle shape and particle size distribution. For dense phase conveying the minimum conveying air velocity can be as low as 3 m/s with many materials, such as cement, fly ash, barytes and bentonite. For design purposes a value of conveying line inlet air velocity, C1, would be taken as the minimum conveying air velocity plus a 20 per cent margin:
It is clearly not advisable to use the minimum value of conveying air velocity for design purposes. The margin is to allow for surges in material flow rate and a safety fac- tor. A surge in material flow rate will cause an increase in pressure, and this will result in a slight reduction in conveying air velocity from two separate sources. One is due to the problems of compressibility of air (see Equation (9.11) and Figure 9.9) and the other is due to the operating characteristics of the compressor (see Figures 6.3 and 6.5).
An additional problem with dense phase conveying, in sliding bed flow for powdered materials, is that the minimum value of conveying air velocity is dependent upon the solid loading ratio and so in this case an initial estimate will have to be made. This relationship has already been illustrated three times, because of its importance, and so it is not reproduced again here for reference. In Figure 8.1 the relationship for all three modes of conveying was included for comparison purposes, in Figure 13.5 the transitional relationship between dilute and dense phase conveying was high- lighted for cement, and then in Figure 14.2 specific data for cement and potassium sulphate was presented. The maximum value of solids loading ratio that can be achieved with a material, conveyed in dense phase sliding bed flow, is dependent upon the pressure gradient available and this was illustrated in Figure 1.1.
For most materials the value of conveying line inlet air velocity that is used is that given by Equation (15.1). An unnecessarily high margin is not recommended because of the adverse effect of velocity on conveying performance, as has been adequately illus- trated with the multitude of conveying characteristics presented. For a few materials, however, this is not necessarily the case. These are materials that can be conveyed at low velocity and show pressure minimum points in their conveying characteristics. These include polyethylene pellets in Figure 12.11c, PVC and PTA in Figure 12.19, and nylon pellets in Figure 13.10. With these materials the optimum point may be chosen, or a lower velocity, particularly if there is a concern about degradation of the material.
To cater for the variation of minimum conveying air velocity with solids loading ratio, for materials capable of being conveyed in dense phase in sliding bed flow, a check and feedback loop are incorporated into the logic diagram. It is unlikely that a correct estimate of the value to be taken for conveying line inlet air velocity would be made in the first instance. Also, if a review of alternative conveying parameters is being undertaken, different air supply pressures will result, and these will give differ- ent pressure gradients. Solids loading ratio, in turn, is dependent upon pressure gradient, and minimum conveying air velocity is dependent upon solids loading ratio.
Calculate air mass flow rate
The determination of the air mass flow rate is the first stage in evaluating the solids loading ratio and providing a check on the value of the conveying line inlet air velocity. Air mass flow rate can be evaluated from the Ideal Gas Law and this was presented in Equation (9.4). This was developed into an expression in terms of the conveying line inlet air velocity with Equation (9.19) and this is reproduced here as Equation (15.2):
where C1 is the conveying line inlet air velocity (m/s); m·a, air mass flow rate (kg/s); R, characteristic gas constant (kJ/kg . K); T1, conveying line inlet temperature (K); d, pipeline bore (m) and p1, conveying line inlet air pressure (kN/m2).
Re-arranging this equation in terms of the air mass flow rate and substituting
where d is the the pipeline bore selected at stage 4; C1, the conveying line inlet air velocity selected at stage 6; p1, for a negative pressure system will be equal to the atmospheric pressure, patm, of 101.3 kN/m2 abs or the appropriate local value if at ele- vation and for a positive pressure system will be equal to patm + 100 L1p, where L1p is the conveying line pressure drop (in bar) selected at stage 5.
Calculate solids loading ratio
Solids loading ratio, ¢, is the ratio of the material flow rate, mp, specified at stage 2 to the air mass flow rate, . , calculated at stage 7. For consistency in units:
Check conveying line inlet air velocity
This is the first of the loops in this logic diagram used to provide a check on the input data for which an initial estimate was necessary. This particular check is for conveying line inlet air velocity and so only applies to materials that are capable of being conveyed in dense phase, as discussed at stage 6. For such materials the value of minimum con- veying air velocity, and hence conveying line inlet air velocity, is dependent upon the value of solids loading ratio.
Having evaluated solids loading ratio at stage 8, the value obtained can be used to determine the corresponding value of conveying line inlet air velocity. This can either be by means of a relationship such as that shown in Figure 13.5 for the material, or some equation of the form:
where C1 is the conveying line inlet air velocity and ¢, the solids loading ratio.
If the value of conveying line inlet air velocity, corresponding to the solids loading ratio for the material, differs from that of the initial estimate, it will be necessary to return to stage 6. The new value can be used as a guide for the next value to be selected, and then the process from stage 6 can be repeated. This is an iterative process that does not converge quickly, and so the next value of conveying line inlet air velocity to be selected must be judged on the basis of previous results, and not simply be a transfer of the result obtained from the check carried out.
If the material has no dense phase conveying potential, or the pressure gradient is such that the material can only be conveyed in dilute phase suspension flow, this particular operation is not necessary. The value chosen will not change to any significant degree over the range of solids loading ratio values that will be possible with the material.
Check conveying line pressure drop
At this point a value for all the main parameters will be available and so a check can be made of the value of conveying line pressure drop selected. Mathematical models for system design are generally in terms of evaluating the conveying line pressure drop for a given set of conditions. The model used, therefore, can be applied to the system and the resulting value of conveying line pressure drop can be checked against that selected at stage 5.
If the value determined by means of the model used differs from that selected it will be necessary to return to stage 5. This is the second of the loops in the logic diagram used to provide a check on the input data from which an initial estimate was necessary. The process is similar to that described above for conveying line inlet air velocity.
Re-specify material mass flow rate
If the check on conveying line pressure drop is close to the original estimate, it will only be necessary to return to stage 5 and select a new value. If the check shows a con- siderable discrepancy, however, it may be necessary to think in terms of a totally dif- ferent system, for which a change in material flow rate may be required, in addition to a change in conveying line pressure drop, for the current bore of pipeline.
If, for example, an original estimate for conveying line pressure drop was 0.8 bar, and the check revealed that for the specified conditions it would actually be two or three times greater than this, then a change in system could be considered. At 0.8 bar a con- tinuously operating system with a low pressure rotary valve and positive displacement blower would be appropriate. With a very much higher operating pressure, a system based on blow tanks, or a high pressure screw or rotary valve would need to be con- sidered, along with a screw compressor. In the case of a high pressure blow tank the material mass flow rate would need to be modified, as discussed earlier at stage 2.
Re-select pipeline bore
If the value of conveying line pressure drop that results from the analysis at stage 10 is not satisfactory, then it will be necessary to select another pipeline bore if the alter- natives at stage 11 are not acceptable. If, for example, the design is to be restricted to a low pressure continuously operating system, then a larger pipeline bore will have to be selected at stage 4 and the analysis from there will have to be repeated.
Calculate power required
Having evaluated all the parameters necessary for the system, it is now possible to deter- mine the power required, and hence the approximate cost associated with operating the system. For an accurate assessment of the power it will be necessary to consult manufac- turers’ literature. By this means different machines capable of meeting the duty could be compared. For a quick, approximate assessment, to allow a comparison to be made of dif- ferent variables in the design, a simple model based on isothermal compression could be used. Such a model was presented in Equation (6.6) and is reproduced here for reference:
is the air mass flow rate (kg/s); p3, compressor inlet pressure (kN/m2 abs) and p4, compressor delivery pressure (kN/m2 abs).
The air mass flow rate in kg/s was evaluated at stage 7, but an allowance should be made for any air leakage across rotary valves, etc. The pressure difference across the compressor, p4 – p3, equates to the conveying line pressure drop at stage 5, but an allowance should be made for any pressure drop across the feeder, filter and any air supply and extraction lines. One of these values is usually atmospheric pressure.
System re-assessment
It was shown with Figure 14.11 that a wide range of combinations of pipeline bore and conveying line pressure drop values could be obtained that would meet a required duty. It was further shown with Figure 14.12 that the power required would probably vary from one set of design parameters to another, and that material type has a very significant influence on the relationship. This loop is added here to allow a full survey to be made, so that the most suitable combination of parameters will ultimately be selected.
The starting point in carrying out a further analysis is to select a different pipeline bore. This will result in a different conveying line pressure drop and so allow a full picture to emerge for the system. It should be noted that pipeline bore is positioned before conveying line pressure drop in this logic diagram since pipes are only avail- able in incremental sizes, whereas conveying line pressure drop is infinitely variable.
Specify pipeline bore required
The final requirement in the design process is to specify the pipeline bore required and the necessary rating of the air mover. If the full analysis has been carried out, as speci- fied in this logic diagram, then the most suitable pipeline size should result. If the pipeline is required to handle more than one material, however, a compromise may well have to be made on both pipeline bore and air requirements, Problems associated with multiple material handling are considered in Chapter 19.
Specify air requirements
Air requirements are specified in terms of volumetric flow rate and delivery or exhaust pressure. The air mass flow rate was evaluated at stage 7 and the relationship between mass and volumetric flow rates is given by:
is the air mass flow rate (kg/s); p, density of air (kg/m3) and V, volumetric flow rate of air (m3/s).
It is the volumetric flow rate at free air conditions, V0, that is required and so the corresponding density of air at free air conditions is needed. This was evaluated at Section 10.2.1.2 as 1.225 kg/m3. Note that the reciprocal of this is referred to as specific volume and is 0.818 m3/kg at free air conditions.
In systems where there is likely to be an air leakage, at the material feed point in the case of positive pressure systems, and at the material discharge point in vacuum systems, an allowance for this must be made in the specification of the volumetric air flow rate required. The delivery or exhaust pressure required is equal to the conveying line pressure drop, plus an allowance for air filtration, the feeding device, air supply and exhaust lines and safety margin. Having determined the necessary air requirements the most appropriate choice of air mover can be made. The capabilities and perform- ance of a number of different types of air mover were considered in Chapter 6.
Logic diagram for system capability
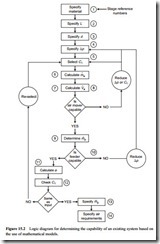
A logic diagram, based on the use of mathematical models, for determining the cap- ability of an existing pneumatic conveying system is presented in Figure 15.2. This type of analysis is generally required in situations where a change in use or layout of a pneumatic conveying system is involved. If a given system is required to convey a different material, or if a shortening or extension of the conveying line is made, it would be well worthwhile carrying out such an analysis in order to provide a check on the air requirements, in addition to determining the new flow rate of the material.
Specify material to be conveyed
This specification is the same as that for stage 1 in the previous logic diagram.
Specify conveying distance
This specification is the same as that for stage 3 in the previous logic diagram.
Specify pipeline bore
For an existing system the pipeline bore will not be a variable. If the resulting flow rate with the new material in the existing system is insufficient, however, it may be necessary to consider installing a pipeline with a larger bore. In this case the design procedure outlines previously in Figure 15.1 for basic system design will be more appropriate, although reference to Chapter 21 on the ‘Optimising and Up-Rating of Existing Sys- tems’ would probably be the best starting point since a change of pipeline bore would also influence the air mover specification, as well as that of the filtration plant.
Specify maximum value of conveying line pressure drop
For an existing system an air mover will be available. It is suggested that, as a starting point in the analysis, the maximum pressure rating of the air mover should be used. The corresponding maximum value of conveying line pressure drop can be obtained by subtracting appropriate pressure drop allowances for pipeline feeding, air separation, transmission losses and operating safety margin, as discussed in relation to power require- ments at stage 13 in connection with system design for the previous logic diagram. As this represents the upper limit available any necessary changes will be to a lower value.
Select conveying line inlet air velocity
Once again the same basic philosophy of matching conveying line inlet air velocity with solids loading ratio, as expounded at stage 6 in the previous logic diagram applies. This, of course, is only the case for materials that have dense phase conveying potential.
With an existing system the capabilities of the air mover have to be considered. As a starting point in the analysis, therefore, it is suggested that the maximum velocity available should be used, or the maximum velocity necessary for the material if this is lower. As this represents the highest value available, or necessary, any subsequent changes will only be to lower values.
Calculate air mass flow rate
The air mass flow rate, m·a, can be evaluated using Equation (15.3) presented above.
Calculate volumetric air flow rate The volumetric flow rate of the air, Va, at free air conditions, V0, can be determined
from the air mass flow rate evaluated in the previous stage, using a re-arrangement of Equation (15.8):
The constant of 0.816 is the value of the specific volume of the air at free air conditions and has the units of m3/kg.
Is the air mover capable?
At stage 4 the conveying line pressure drop was specified, and hence the supply or exhaust pressure can be obtained, and the volumetric flow rate was determined at stage 7. With an existing system it is necessary to check that the requirements are within the capabilities of the air mover, and the above parameters are those necessary for such a check to be made.
In the first instance the conveying line pressure drop and conveying line inlet air velocity are chosen to ensure that this is the case. If at a subsequent stage, the rela- tionship between conveying line inlet air velocity and solids loading ratio is not satis- fied and it is necessary to make changes, then a further check is advisable. If it is found that the air mover is not capable, a reduction will have to be made in either the con- veying line pressure drop or the conveying line inlet air velocity.
The possibility of a reduction in conveying line inlet air velocity will depend upon the value of the solids loading ratio to be evaluated at stage 11. If a reduction in con- veying line inlet air velocity cannot be made, then a reduction in conveying line pres- sure drop will have to be made. In addition to satisfying the conveying requirements, the characteristics of the air mover will also have to be consulted in order to check on the possibility of making such changes.
Determine material flow rate
At this point a value of all the main parameters is available, with the exception of the solids loading ratio, but since m·p = ¢ X m·a by definition, a simple relationship exists
that should present no difficulty in incorporating. It should be possible, therefore, with the appropriate model, to evaluate the material flow rate for the given set of conditions.
Is the material feeding device capable?
If an existing system is required to handle another material, it is quite possible that the material flow rate with the new material could be significantly different from that of the original material. If the new flow rate is lower, or higher, the possibility of using the feeding device satisfactorily must be investigated. If it is established that the feed- ing device has a maximum capability that is less than that of the pipeline system with the new material, then a reduction in conveying line pressure drop should be made in order to reduce the capability of the pipeline to match that of the feeder. If this is done it should result in a saving in operating power. In the case of positive displacement feeders the bulk density of the new material must also be taken into account.
Calculate solids loading ratio
This is evaluated in the same way as described at stage 8 in the previous logic diagram with Equation (15.4).
Check conveying line inlet air velocity
Having determined the material flow rate at stage 9, and then the solids loading ratio at stage 11, it is now possible to check the value of conveying line inlet air velocity at stage 5. This process is the same as that outlined at stage 9 for the previous logic diagram.
Specify material flow rate
When a check at stage 12 is obtained between solids loading ratio and conveying line inlet air velocity, the process will be complete. The final value of material flow rate determined at stage 9 can be specified as the actual rating of the system with the given material.
Specify air requirements
A loop is built into the logic diagram to ensure that the air mover is capable of meet- ing the required demand. It is quite possible, however, that some changes may have to be made, such as restricting delivery pressure, restricting flow rate, changing drive speed, etc, and so this will need to be clearly specified.